什么是仙人掌

仙人掌是一种带刺的图, 它可以让你浑身都不舒服
仙人掌是一种连通图, 没有一条边同时属于两个简单环. 形象地表示一下, 就又要祭出这张经典图了:

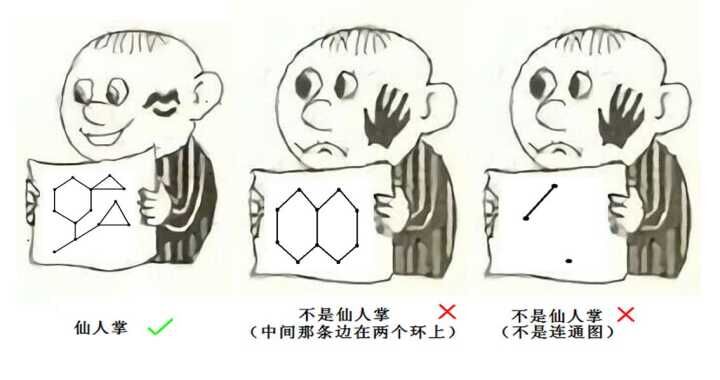
那么仙人掌有什么特点, 使得它被毒瘤出题人钟爱呢? 这就要谈到种植仙人掌的姿势了:
准备一个瓦盆, 在里面填上沙壤土, 将仙人掌种进去, 平时少浇水多晒太阳

圆方树

圆方树, 即将仙人掌化成一棵树, 而树上问题非常经典, 于是出题人就可以把一些树上问题搬到仙人掌上, 然后来恶心选手辣!
圆方树即原仙人掌中的点为圆点, 对于每一个环, 添加一个方点, 方点与所有环上的圆点相连, 没有两个方点会相连. 如图:

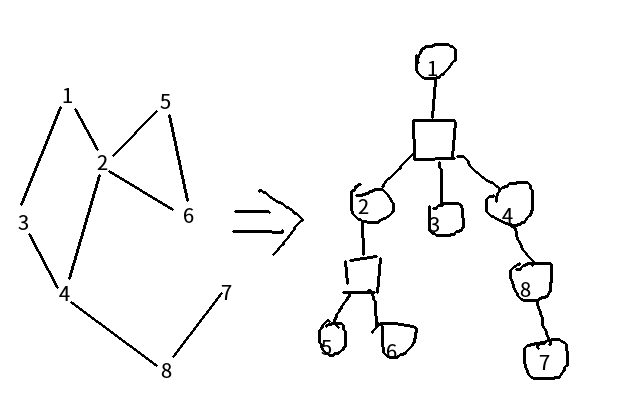
当然了, 在圆方树上解决问题的时候, 一定要特别考虑方点对于问题带来的影响.
如何种植圆方树呢? 跑 tarjan 双连通分量找环先考虑不在环上的点再考虑在环上的, 正当 litble 这么想着的时候, 一位不愿透露姓名的 Cai 大佬跑过来, 大喊:” 打圆方树居然用 tarjan?! 你是人吗?”
失去做人资格的 litble 又向 Cai 大佬请教了一发,get 了 Cai 大佬由于打挂了 tarjan 很不爽而发明的不用 tarjan 的构造圆方树的方法:
1. 遍历仙人掌，同时打上时间戳
2. 假如遇到了一个时间戳比在当前点 x 小的点，说明发现了一个环，暴力将该环打上 “是环” 的标记，同时环顶要打上不同的标记
3. 继续遍历仙人掌，并标记每个点的 “父亲” 即来时的节点
4. 回溯时，如果发现该点有环上信息标记，则不用将该点与父亲连边，取消标记。如果是环顶，则暴力处理环的一些相关内容，如建立方点等。

void btree(int x,int las) {//构建圆方树，las: 记录来时的边
    vis[x]=++tim;//打时间戳
    for(int i=hh[x];i;i=nn[i]) 
        if((i^1)!=las) {
        if(vis[tt[i]]&&vis[tt[i]]>vis[x]) continue;
        if(vis[tt[i]]) ks[tt[i]]=ww[i],mc(x,tt[i]);//ks,kl：存环上的距离信息，mc: 暴力标记环
        if(!vis[tt[i]]) pre[tt[i]]=x,kl[tt[i]]=ww[i],btree(tt[i],i);//递归处理
        if(cir[x]==-1) {cir[x]=0;continue;}
        if(cir[x]) {dc(cir[x],x),cir[x]=0;continue;}//对环进行处理
        link(x,tt[i],ww[i]);//连边
    }
}

例题:bzoj2125。
圆点和圆点之间的边权就是原图的边权，圆点到儿子方点的距离为 0，方点到儿子圆点的距离为原仙人掌上该圆点到方点的父亲（一个圆点）的环上最短距离。
然后对于每组询问求 LCA，如果 LCA 是圆点，距离很好弄，是方点，就看在求 LCA 的路径上经过的那两个圆点，通过环上前缀和的方式求出它们之间的最短距离。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
const int N=10005,M=50005,NN=20005;;
int n,m,Q,t0=1,tim,sz,tot;
int hh[N],tt[M],nn[M],ww[M],vis[N],pre[N],cir[N],kl[N],ks[N];
int h[NN],to[NN],ne[NN],w[NN];LL s[NN];
void add(int x,int y,int z) {tt[++t0]=y,nn[t0]=hh[x],hh[x]=t0,ww[t0]=z;}
void link(int x,int y,int z) {to[++tot]=y,ne[tot]=h[x],h[x]=tot,w[tot]=z;}
void mc(int x,int y) {cir[y]=x;while(x!=y) cir[x]=-1,x=pre[x];}//对环做标记
void dc(int x,int y) {//处理环，建立方点和环上前缀和
    ++sz,link(y,sz,0);int sum=ks[y],t=x;
    while(x!=y) s[x]=sum,sum+=kl[x],x=pre[x];
    s[sz]=sum;
    while(t!=y) link(sz,t,min(s[t],s[sz]-s[t])),t=pre[t];
}
void btree(int x,int las) {//构建圆方树
    vis[x]=++tim;
    for(int i=hh[x];i;i=nn[i]) 
        if((i^1)!=las) {
        if(vis[tt[i]]&&vis[tt[i]]>vis[x]) continue;
        if(vis[tt[i]]) ks[tt[i]]=ww[i],mc(x,tt[i]);//ks,kl：存环上的距离信息
        if(!vis[tt[i]]) pre[tt[i]]=x,kl[tt[i]]=ww[i],btree(tt[i],i);
        if(cir[x]==-1) {cir[x]=0;continue;}
        if(cir[x]) {dc(cir[x],x),cir[x]=0;continue;}
        link(x,tt[i],ww[i]);
    }
}
LL dis[NN];int f[NN][16],dep[NN];
void dfs(int x,int las) {
    f[x][0]=las,dep[x]=dep[las]+1;
    for(int i=1;i<=15;++i) f[x][i]=f[f[x][i-1]][i-1];
    for(int i=h[x];i;i=ne[i])
        if(to[i]!=las) dis[to[i]]=dis[x]+(LL)w[i],dfs(to[i],x);
}
int lca(int x,int y,int &ka,int &kb) {
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=15;i>=0;--i) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
    if(x==y) return x;
    for(int i=15;i>=0;--i)
        if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    ka=x,kb=y;return f[x][0];
}
int main() {
    int x,y,z,ka,kb;
    n=read(),m=read(),Q=read();
    for(int i=1;i<=m;++i) {
        x=read(),y=read(),z=read();
        add(x,y,z),add(y,x,z);
    }
    sz=n,btree(1,0),dfs(1,0);
    while(Q--) {
        x=read(),y=read(),z=lca(x,y,ka,kb);
        if(z<=n) printf("%lld\n",dis[x]+dis[y]-dis[z]*2);
        else {//如果 lca 是方点
            LL ans=dis[x]+dis[y]-dis[ka]-dis[kb];
            ans+=min(abs(s[ka]-s[kb]),s[z]-abs(s[ka]-s[kb]));
            printf("%lld\n",ans);
        }
    }
    return 0;
}

仙人掌生成器

在打第一道仙人掌题的时候, 蒟蒻 litble 就各种 GG, 于是膜了一发仙人掌生成器.VFK 应该在他的 uojblog 里说过一种生成仙人掌的方法, 但是还有一种方法是:
构建一棵树, 将若干不相邻的点改成方点, 然后把圆方树还原成一棵仙人掌.
以下是上面那道例题的数据生成器.

#include<bits/stdc++.h>
using namespace std;
const int N=100005,M=200005;
int n,m,tot,js,tn,q;
int f[N],bj[N],h[N],to[N],ne[N],u[M],v[M],pos[N];
void add(int x,int y) {to[++tot]=y,ne[tot]=h[x],h[x]=tot;}
void dfs(int x,int las) {
    if(!bj[x]) pos[x]=++tn;//点的重标号
    int tmp=las;
    for(int i=h[x];i;i=ne[i]) {
        if(to[i]==las) continue;
        dfs(to[i],x);
        if(!bj[x]&&!bj[to[i]]) u[++m]=pos[x],v[m]=pos[to[i]];//不在环上的边
        if(bj[x]) u[++m]=pos[tmp],v[m]=pos[to[i]],tmp=to[i];//对于方点, 搞出环
    }
    if(bj[x]&&tmp!=las) u[++m]=pos[tmp],v[m]=pos[las];
}
int check(int x) {
    if(x==1) return 0;
    if(bj[f[x]]) return 0;
    for(int i=h[x];i;i=ne[i])
        if(bj[to[i]]) return 0;
    return 1;
}
int main()
{
    srand(time(0));
    n=rand()%12+3,js=rand()%(n-2)+1,q=rand()%10+1;//n: 树的点数,js: 方点个数
    for(int i=2;i<=n;++i) f[i]=rand()%(i-1)+1,add(f[i],i);//生成一棵树
    for(int i=1;i<=js;++i) {
        int x=rand()%(n-1)+2;//圆方树的根一定要是圆点
        if(check(x)) bj[x]=1;//check: 判断是否可以是方点
    }
    dfs(1,0);
    printf("%d %d %d\n",tn,m,q);//输出结果
    for(int i=1;i<=m;++i) printf("%d %d %d\n",u[i],v[i],rand()%10+1);
    for(int i=1;i<=q;++i) {
        int x=rand()%tn+1,y=rand()%tn+1;
        while(y==x) y=rand()%tn+1;
        printf("%d %d\n",x,y);
    }
    return 0;
}

仙人掌的应用

准确的来说，仙人掌只是一种出题人无聊的时候整一整的东西，没有任何实际应用价值，不过，我还说说一说吧。

bzoj4316

圆方树的树形 dp, 可以设 $f(i,0)$: 不选 i 的情况下，i 的子树里最多可以选多少点。$f(i,1)$: 不选 i
对于圆点，就是最普通的树形 dp。对于方点，我们可以先看看这个环，环顶（方点的父亲）的点和某一个与环顶相连的点里，一定有一个不选，那么我们设强制不选环顶或者强制不选环底（即那个与环顶相连的点），跑两次 dp 更新方点父亲的 dp 值。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
const int N=50005,M=120005,inf=0x3f3f3f3f;
int h1[N],h2[N<<1],vis[N],cir[N],pre[N];
int f[N<<1][2],g[N<<1][2],st[N<<1];
struct edge{int ne,to;}e1[M],e2[N<<1];
int n,m,t1=1,t2,tim,sz;
void ad1(int x,int y) {e1[++t1].to=y,e1[t1].ne=h1[x],h1[x]=t1;}
void ad2(int x,int y) {e2[++t2].to=y,e2[t2].ne=h2[x],h2[x]=t2;}
void mc(int x,int y) {cir[y]=x;while(x!=y) cir[x]=-1,x=pre[x];}
void dc(int x,int y) {++sz,ad2(y,sz);while(x!=y) ad2(sz,x),x=pre[x];}
void btree(int x,int las) {//建立圆方树
    vis[x]=++tim;
    for(int i=h1[x];i;i=e1[i].ne)
        if((i^1)!=las) {
        if(vis[e1[i].to]&&vis[e1[i].to]>vis[x]) continue;
        if(vis[e1[i].to]) mc(x,e1[i].to);
        if(!vis[e1[i].to]) pre[e1[i].to]=x,btree(e1[i].to,i);
        if(cir[x]==-1) {cir[x]=0;continue;}
        if(cir[x]) {dc(cir[x],x),cir[x]=0;continue;}
        ad2(x,e1[i].to);
    }
}
void dp(int x,int las) {
    if(x<=n) {//圆点直接 dp
        f[x][0]=0,f[x][1]=1;
        for(int i=h2[x];i;i=e2[i].ne) {
            int y=e2[i].to;dp(y,x);
            if(y<=n) f[x][0]+=max(f[y][0],f[y][1]),f[x][1]+=f[y][0];
        }
        return;
    }
    int top=0,t0,t1;//处理方点
    for(int i=h2[x];i;i=e2[i].ne) dp(e2[i].to,x);
    for(int i=h2[x];i;i=e2[i].ne) st[++top]=e2[i].to;//不可与上一句同写
    st[++top]=las,g[st[1]][0]=f[st[1]][0],g[st[1]][1]=-inf;//不选环底
    for(int i=2;i<=top;++i) {
        g[st[i]][0]=f[st[i]][0]+max(g[st[i-1]][0],g[st[i-1]][1]);
        g[st[i]][1]=f[st[i]][1]+g[st[i-1]][0];
    }
    t0=max(f[las][0],g[las][0]),t1=max(f[las][1],g[las][1]);
    g[st[1]][0]=f[st[1]][0],g[st[1]][1]=f[st[1]][1];//不选环顶
    for(int i=2;i<=top;++i) {
        g[st[i]][0]=f[st[i]][0]+max(g[st[i-1]][0],g[st[i-1]][1]);
        g[st[i]][1]=f[st[i]][1]+g[st[i-1]][0];
    }
    f[las][0]=max(t0,g[las][0]),f[las][1]=t1;
}
int main() {
    int x,y; n=read(),m=read();
    for(int i=1;i<=m;++i) x=read(),y=read(),ad1(x,y),ad1(y,x);
    sz=n,btree(1,0),dp(1,0);
    printf("%d\n",max(f[1][0],f[1][1]));
    return 0;
}

bzoj1023

同样也是圆点直接 dp，方点弄个单调队列，考虑环上的两个点之间的距离怎样最近（显然两个环上的点之间有两条路），然后 dp 两次即可。

#include<bits/stdc++.h>
using namespace std;
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
const int N=50005;
int n,m,t1=1,t2,tim,sz,ans;
int h1[N],h2[N<<1],vis[N],cir[N],pre[N],f[N<<1],st[N<<1];
int Q[N<<1],ss[N<<1];
struct edge{int to,ne;}e1[N<<2],e2[N<<1];
void ad1(int x,int y) {e1[++t1].to=y,e1[t1].ne=h1[x],h1[x]=t1;}
void ad2(int x,int y) {e2[++t2].to=y,e2[t2].ne=h2[x],h2[x]=t2;}
void mc(int x,int y) {cir[y]=x;while(x!=y) cir[x]=-1,x=pre[x];}
void dc(int x,int y) {++sz,ad2(y,sz);while(x!=y) ad2(sz,x),x=pre[x];}
void btree(int x,int las) {
    vis[x]=++tim;
    for(int i=h1[x];i;i=e1[i].ne)
        if((i^1)!=las) {
        if(vis[e1[i].to]&&vis[e1[i].to]>vis[x]) continue;
        if(vis[e1[i].to]) mc(x,e1[i].to);
        if(!vis[e1[i].to]) pre[e1[i].to]=x,btree(e1[i].to,i);
        if(cir[x]==-1) {cir[x]=0;continue;}
        if(cir[x]) {dc(cir[x],x),cir[x]=0;continue;}
        ad2(x,e1[i].to);
    }
}
void dp(int x) {
    if(x<=n) {
        int mx1=0,mx2=0;
        for(int i=h2[x];i;i=e2[i].ne) {
            dp(e2[i].to);
            if(f[e2[i].to]+1>=mx1) mx2=mx1,mx1=f[e2[i].to]+1;
            else if(f[e2[i].to]+1>mx2) mx2=f[e2[i].to]+1;
        }
        ans=max(ans,mx1+mx2),f[x]=mx1;
        return;
    }
    int top=0,he=1,ta=0;
    for(int i=h2[x];i;i=e2[i].ne) dp(e2[i].to);
    for(int i=h2[x];i;i=e2[i].ne) st[++top]=e2[i].to;
    for(int i=1;i<=top;++i) {//方点第一次 dp
        while(he<=ta&&i-Q[he]>top+1-i+Q[he]) ++he;
        if(he<ta) ans=max(ans,f[st[i]]+f[st[Q[he]]]+i-Q[he]);
        while(he<=ta&&f[st[i]]-i>=f[st[Q[ta]]]-Q[ta]) --ta;
        Q[++ta]=i;
    }
    he=1,ta=0;
    for(int i=top;i>=1;--i) {//方点第二次 dp
        while(he<=ta&&i-Q[he]<top+1-i+Q[he]) ++he;
        if(he<ta) ans=max(ans,f[st[i]]+f[st[Q[he]]]+top+1-i+Q[he]);
        while(he<=ta&&f[st[i]]+i>=f[st[Q[ta]]]+Q[ta]) --ta;
        Q[++ta]=i;
    }
    for(int i=1;i<=top/2;++i) f[x]=max(f[x],i+f[st[i]]-1);
    for(int i=top/2+1;i<=top;++i) f[x]=max(f[x],top-i+f[st[i]]);
}
int main() {
    int num,x,y;
    n=read(),m=read();
    for(int i=1;i<=m;++i) {
        num=read();
        for(int j=1;j<=num;++j,y=x)
            {x=read(); if(j!=1) ad1(y,x),ad1(x,y);}
    }
    sz=n,btree(1,0),dp(1);
    printf("%d\n",ans);
    return 0;
}