1. 题目
推荐看 BZOJ – 2648 的题面,BZOJ – 2716 的样例,,,呵呵,神经病出的样例,出个 100 组的样例给你有啥用,真不知道出题人怎么想的,这么毒瘤真的有什么用吗?
题意:给出平面上多个点,每次询问一个坐标,求给出的点中到该坐标的曼哈顿距离最小是多少。
2. 题解
听说 CDQ 能做 QvQ
但是听说 CDQ 会在 BZOJ – 2648 被卡TLE。。。
KD-Tree 还是很吼滴!
根据 KD-Tree 的思想,每次会取出中间的一个点,把整个大矩形分成两个小矩形(这里的矩形指的是——将该子树所代表的点集全部覆盖的最小矩形)。
而且,,,KD-Tree 靠的是玄学
所以我们维护每棵子树所对应的矩形。
对于每一个询问的坐标,我们可以算出这个矩形到该坐标的曼哈顿距离!
什么叫做矩形到坐标的曼哈顿距离呢?
就是矩形所包含的所有点中到该坐标的曼哈顿距离的最小值(不一定是之前已经存在的点,而是所有的点,包括实数坐标的点)。
比如下图所示:
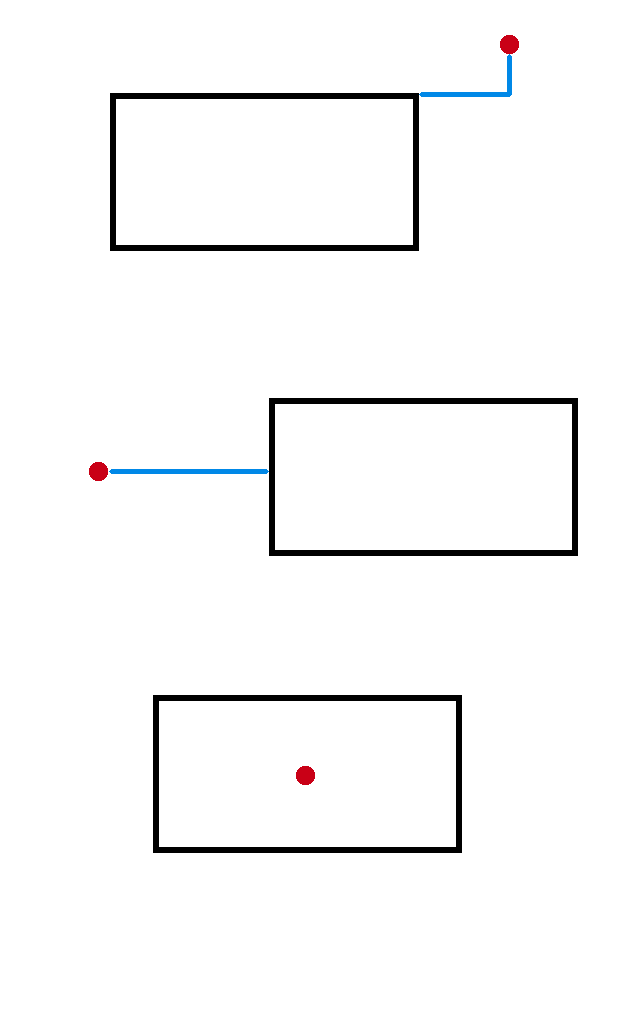
(其中黑色线是矩形,红色是询问的坐标点,蓝色线是距离,而第三个距离为 0)
我们由此可以来对 KD-Tree 剪枝(因为答案必然大于等于该坐标到矩形的最小曼哈顿距离)
这样复杂度最坏是 $O(n\sqrt n)$的(鬼知道怎么证,反正就是这样子的)。
注意是最坏复杂度,实际上复杂度远低于它 QvQ
其实是 $O(XuanXue)$的吧 QvQ
至于 KD-Tree 的平衡,这题数据是随机的,不平衡它是最快的,,,平衡了反而慢了。。。
如果你像我一样真的喜欢平衡树的话,就像替罪羊一样平衡它吧,看它不爽(破坏了平衡阀值)就拍扁它(先序遍历成一个序列)再重构(Build)。
我试过了,有序插入的话不平衡真的会挂掉啊。。。
题目真良心。。。
代码:
#include <bits/stdc++.h>
#define NS (500005)
#define DS (2)
#define AS (0.75)
using namespace std;
template <typename _Tp>inline void IN (_Tp& dig)
{
char c; bool flag = 0; dig = 0;
while (c = getchar(), !isdigit(c)) if (c == '-') flag = 1;
while (isdigit(c)) dig = dig * 10 + c - '0', c = getchar();
if (flag) dig = -dig;
}
int n, m, root, sz, D;
stack<int> rub;
int MKN()
{
if (rub.empty()) return ++sz;
int tmp = rub.top(); rub.pop(); return tmp;
}
struct node
{
int d[DS], mx[DS], mn[DS], l, r, sz;
int& operator [] (int a) {return d[a];}
bool operator < (node another)const {return d[D] < another[D];}
}arr[NS << 1], e[NS << 1];
void pup(int a)
{
node l = e[e[a].l], r = e[e[a].r];
for (int i = 0; i < DS; i += 1)
{
e[a].mx[i] = e[a].mn[i] = e[a][i];
if (e[a].l)
{
e[a].mx[i] = max(e[a].mx[i], l.mx[i]);
e[a].mn[i] = min(e[a].mn[i], l.mn[i]);
}
if (e[a].r)
{
e[a].mx[i] = max(e[a].mx[i], r.mx[i]);
e[a].mn[i] = min(e[a].mn[i], r.mn[i]);
}
}
e[a].sz = l.sz + r.sz + 1;
}
int Build(int l, int r, int d = 0)
{
if (l > r) return 0;
D = d;
int a = MKN(), mid = ((l + r) >> 1);
nth_element(arr + l, arr + mid, arr + r + 1);
e[a] = arr[mid];
e[a].l = Build(l, mid - 1, (d + 1) % DS);
e[a].r = Build(mid + 1, r, (d + 1) % DS);
pup(a); return a;
}
void rec(int a,int tot = 0)
{
if (!a) return;
rec(e[a].l, tot), tot += e[e[a].l].sz + 1;
arr[tot] = e[a], rub.push(a);
rec(e[a].r, tot);
}
void check(int& a, int d)
{
if (e[e[a].l].sz > e[a].sz * AS || e[e[a].r].sz > e[a].sz * AS)
rec(a), a = Build(1, e[a].sz, d);
}
void insert(node T, int& a = root, int d = 0)
{
if (!a)
{
a = MKN(), e[a] = T, e[a].l = e[a].r = 0, pup(a);
return;
}
if (T[d] < e[a][d]) insert(T, e[a].l, (d + 1) % DS);
else insert(T, e[a].r, (d + 1) % DS);
pup(a), check(a, d);
}
int dis(node T, int a)
{
int tot = 0;
for (int i = 0; i < DS; i += 1)
tot += abs(T[i] - e[a][i]);
return tot;
}
int get_dis(node T, int a)
{
int tot = 0;
for (int i = 0; i < DS; i += 1)
tot += max(e[a].mn[i] - T[i], 0) + max(T[i] - e[a].mx[i], 0);
return tot;
}
void query(node T, int& ans, int a = root)
{
ans = min(ans, dis(T, a));
int dl = INT_MAX, dr = INT_MAX;
if (e[a].l) dl = get_dis(T, e[a].l);
if (e[a].r) dr = get_dis(T, e[a].r);
if (dl < dr)
{
if (dl < ans) query(T, ans, e[a].l);
if (dr < ans) query(T, ans, e[a].r);
}
else
{
if (dr < ans) query(T, ans, e[a].r);
if (dl < ans) query(T, ans, e[a].l);
}
}
int main(int argc, char const* argv[])
{
IN(n), IN(m);
for (int i = 1; i <= n; i += 1)
for (int j = 0; j < DS; j += 1)
IN(arr[i][j]);
root = Build(1, n);
while (m--)
{
int opt, a, b, ans = INT_MAX;
IN(opt), IN(a), IN(b);
if (opt == 1) insert((node){a,b});
else printf("%d\n", (query((node){a,b}, ans), ans));
}
return 0;
}
0 条评论