1. 何谓 LCA
LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点 u 和 v 最近的公共祖先。
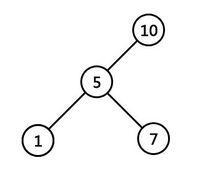
如图,1 和 7 的公共祖先有 5 和 10,而它们的 LCA 是 5。
2. 怎么求 LCA
题设:求节点 a,b 的 LCA
思路 1:从节点 a 遍历到根节点,再从 b 遍历到根节点,找到最先相遇的地方。复杂度:o(n)
思路 2:倍增。具体怎么做底下讲。复杂度:o(log n)
3. 倍增求 LCA
做法:程序开始时选取任意节点为树根,进行 dfs,得到所有点的深度与 pre[i][j]。何谓 pre[i][j]?
pre[i][j] 指节点 i 的第 2 的 j 次方个祖先
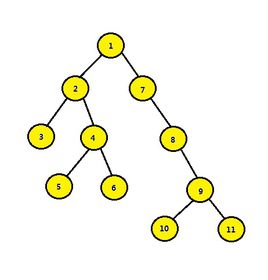
如上图中,10 的第 1 个祖先是 9,第二个祖先是 8,第三个祖先是 7,第四个祖先是 1。所以 10 的第 2 的 0 次方个祖先是 9(2^0=1),10 的第 2 的 1 次方个祖先是 8(2^1=2),10 的第 2 的 2 次方个祖先是 1(2^2=4)。很显然,10 没有 2 的 3 次方个祖先。所以 pre[10][0]=9,pre[10][1]=8,pre[10][2]=1。
而且通过倍增的思想,我们不难发现 i 的第 2 的 j 次方个祖先就是 i 的第 2 的 j-1 次方个祖先的第 2 的 j-1 次方个祖先(不信你看图),所以 pre[i][j]=pre[pre[i][j-1]][j-1]。
其实要搞懂这个也很简单:
2^i = 2*2^(i-1) = 2^(i-1) + 2^(i-1)
懂了吧
所以:
i 的第 2 的 j 次方个祖先就是 i 的第 2 的 j-1 次方个祖先的第 2 的 j-1 次方个祖先
有了这个规律,我们就可以在 dfs 中预处理所有的 pre 了!
而求 LCA 的思路就是:对于节点 a 和 b,先把深度大的节点提升到深度小的节点的相同深度,然后把 a 和 b 同时往上提,每次能提多少提多少,每次提了以后要保证节点 a!=节点 b,提升的高度从大往小找(先找 n,再找 n/2,再找 n/4,再找 n/8,再找 n/16……最后再找 1)。
而最后 LCA 就是 a(或 b)的父节点。
具体实现看代码吧……
4. 例题与代码
HDU – 2586 How far away ?传送门= ̄ω ̄=
思路:对于点 a 和点 b,他们的树上距离是唯一的,也是最小的(因为树上任意两点直接只有一条通路),距离为 a 到根节点的距离+b 到根节点的距离-2×(a 和 b 的 lca 到根节点的距离)(很明显我就不证了^_^)。
注意!点到根节点的距离不同于点的深度!下面的代码中,deep[i] 指节点 i 的深度,而 far[i] 表示节点 i 到根节点的距离!都通过递增得到!(根节点到根节点的距离为 0,根节点的深度也为 0)
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int maxs=40005,logs=20;
int t,n,m,pre[maxs][logs+1],deep[maxs],far[maxs];
vector<int> g[maxs],dis[maxs];
void dfs(int x,int p)
{
pre[x][0]=p;
for(int i=1;i<=logs;i++)pre[x][i]=pre[pre[x][i-1]][i-1];
for(int i=0;i<g[x].size();i++)
if(g[x][i]!=p)
deep[g[x][i]]=deep[x]+1,far[g[x][i]]=far[x]+dis[x][i],dfs(g[x][i],x);
}
int getlca(int a,int b)
{
if(deep[a]>deep[b])swap(a,b);
for(int i=logs;i>=0;i--)if(deep[pre[b][i]]>=deep[a])b=pre[b][i];
if(a==b)return a;
for(int i=logs;i>=0;i--)if(pre[a][i]!=pre[b][i])a=pre[a][i],b=pre[b][i];
return pre[a][0];
}
int main()
{
ios::sync_with_stdio(0);
cin>>t;
while(t--)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
g[i].clear(),dis[i].clear();
for(int j=0;j<=logs;j++)pre[i][j]=0;
}
for(int i=1,a,b,c;i<n;i++)
{
cin>>a>>b>>c;
g[a].push_back(b),g[b].push_back(a);
dis[a].push_back(c),dis[b].push_back(c);
}
dfs(1,0);
for(int i=1,a,b;i<=m;i++)cin>>a>>b,cout<<far[a]+far[b]-2*far[getlca(a,b)]<<endl;
}
return 0;
}
3 条评论
1a · 2019年10月26日 9:44 下午
可以,懂了
juruo-oier · 2018年8月22日 2:58 下午
太强了,这是我看过就懂的求 lca 的方法
XZYQvQ · 2018年8月22日 5:15 下午
emmmmm…
海星.jpg
(其实曾经 litble 大神也表扬过这篇文章只不过在某次博客大爆炸中丢失了)
(话说为啥我以前写的代码这么丑。。。)