算法实现

例题:HDU2255

有一天，CSSYZ 6 机房全体成员要开黑打一场比赛。打比赛的共有 n 个人，比赛一共有 n 道题。由于比赛是 CF 赛制，按照每个人对于每种算法的掌握程度不同，第 i 个人做第 j 道题可以让全体成员获得 x 个积分。显然，每道题只能 A 一次，并且做题比较消耗体力，所以大家决定每人做一道题，使得总积分最大。
首先每个人有个期望得分，大小为该人做所有题目可得积分的最大值，标在了左侧（为了方便起见，先取三个成员为例）。

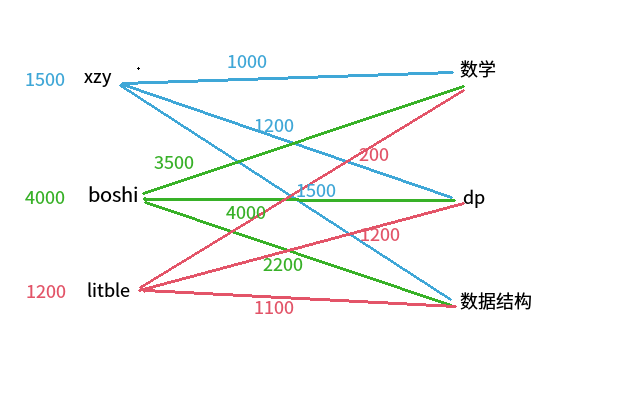
首先，xzy 依次查看所有题目，只有题目的期望得分和他自己的期望得分加起来等于做这道题的可得分，他才会选择该题。所以，xzy 选择数据结构题，同理，boshi 选择 dp 题。

轮到 litble，她想要选择 dp 题，但是 dp 题已经被 boshi 选了，boshi 不可以选其他题。于是，boshi 和 litble 要降低相同的期望，使得有人能够做这一轮查看了但是没有人选的题，也就是数学题。降低的最少期望是 500.

boshi 的期望变成 3500,litble 的期望变成 700. 而被选过了题目，为了保证它本来能够造成的得分贡献不会降低，所以这一轮被选过的题目（dp 题，数据结构题）本身的期望要加上 500.

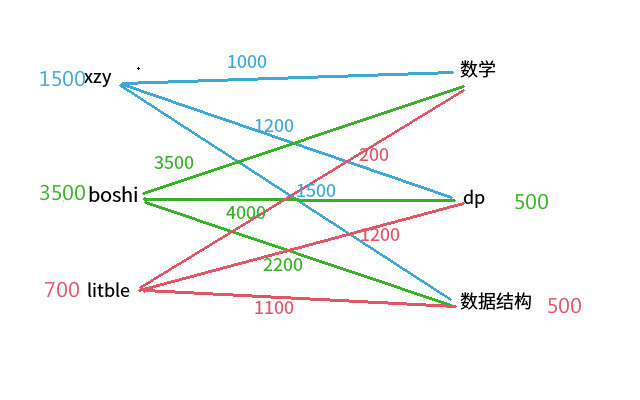
然后litble再次进行选择，看数学题，700>200，不选。看 dp 题，500+700=1200，可以选择。litble 妄图选择 dp 题，于是只能与 boshi 沟通，boshi 此时 3500=3500, 可以选择数学题，于是 boshi 选择了数学题，litble 选择了 dp 题皆大欢喜。

最后这场比赛总得分：1500+3500+1200=6200 分。

由以上这场分配题目的过程，我们可以总结出 KM 算法的写法：

#include<bits/stdc++.h>
using namespace std;
#define RI register int
const int N=305,inf=0x3f3f3f3f;
int w[N][N],expa[N],expb[N],visa[N],visb[N],cp[N],dl[N];
int n;
int dfs(int x) {
    visa[x]=1;
    for(RI i=1;i<=n;++i) {
        if(visb[i]) continue;//不用重复看相同题目
        int kl=expa[x]+expb[i]-w[x][i];
        if(kl==0) {
            visb[i]=1;
            if(!cp[i]||dfs(cp[i])) {cp[i]=x;return 1;}
        }
        else dl[i]=min(dl[i],kl);
    }
    return 0;
}
int work() {
    for(RI i=1;i<=n;++i) expb[i]=expa[i]=cp[i]=0;//题目期望：0
    for(RI i=1;i<=n;++i)//人的期望：他可以做得的最大得分
        for(RI j=1;j<=n;++j) expa[i]=max(expa[i],w[i][j]);
    for(RI i=1;i<=n;++i) {
        for(RI j=1;j<=n;++j) dl[j]=inf;//dl: 没有被选择的题目，如果要让有人能选它，人们需要降低多少期望
        while("niconiconi") {
            for(RI j=1;j<=n;++j) visa[j]=visb[j]=0;//清空 vis
            if(dfs(i)) break;
            int kl=inf;
            for(RI j=1;j<=n;++j) if(!visb[j]) kl=min(kl,dl[j]);
            for(RI j=1;j<=n;++j) {
                if(visa[j]) expa[j]-=kl;//人降低期望
                if(visb[j]) expb[j]+=kl;//被选过的题目升高期望
                else dl[j]-=kl;//由于人降低了期望，所以题目要被人选的分数差距降低了
            }
        }
    }
    int re=0;
    for(RI i=1;i<=n;++i) re+=w[cp[i]][i];
    return re;
}
int main()
{
    while(~scanf("%d",&n)) {
        for(RI i=1;i<=n;++i)
            for(RI j=1;j<=n;++j) scanf("%d",&w[i][j]);
        printf("%d\n",work());
    }
    return 0;
}   

正确性

对于存在争端的两个人，我们为了让有人去选没有那么适合 TA 的题目，需要降低期望。为了防止可得分被抹掉，要降低得尽量少。

而对于一个题目而言，它已经被选过了，已经能够造成一定的贡献。一个新分配方案，有新的题目被选，总得分如果不升反降，自然是不行的。题目的期望值就起到了这个作用，由于题目期望值的约束，新分配方案的权值一定要不降。

时间复杂度

O(跑得过)

O(快于费用流)

大约是 $O(n^2m)$的，对于稠密图可能会变成 $O(n^4)$，这就非常不够优秀。