杜教筛

用途

​ 当数论函数求值这种简单题考地太多了，出题人也觉得无聊。于是就开始研究数论函数的和。

​ 如：求下面式子的值。
$$
\sum _ {i=1}^{n}\phi (i) \ \ \ \ \ \ \ \ \ \ \ \ \ (n < 10^{12})
$$
​ 这一类问题就算利用高效的线性筛我们对他也无能为力。甚至分段打表这种奇技淫巧都拿他没办法。因此我们需要采用一些特殊的做法，将时间复杂度优化至线性以下。

​ 这类做法一般有扩展埃氏筛、杜教筛、洲阁筛等等。其中扩展埃氏筛可扩展性最强。但杜教筛在其领域内仍有扩展埃氏筛无法解决的问题。

​ 杜教筛大概起源于网站 Project Euler，并由 DuYH 引入国内 OI 界。

数论分块

​ 杜教筛的前置技能树并不大，而数论分块是其必备技能之一。

​ 先看如何求前 n 个正整数的约数之和。
$$
\sum_{i=1}^n\sigma(i)\ \ \ \ \ \ \ \ \ \ \ (n < 10^{16})
$$

---

​ 当然，我们需要先对公式变形。

$$
\sum_{i=1}^n\sigma(i)=\sum_{i=1}^n\sum_{i|j}^{j\leq n}i=\sum_{i=1}^ni\cdot\lfloor\frac{n}{i}\rfloor
$$

​ 这里运用了一个常用的数学技巧，简单说就是换个角度看问题。为了求每个数的约数的和，我们不妨枚举约数，统计有多少个数有这个约数。这也就是第一个等号的来由。

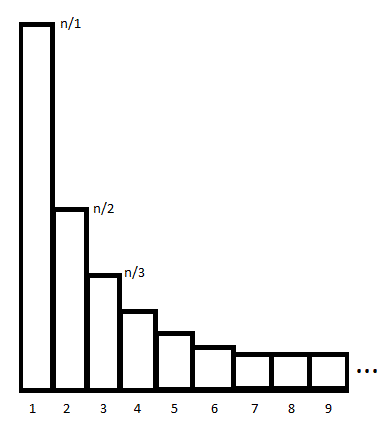
换个角度看问题：下面有 n 堆箱子，第 i 堆的箱子数是 $\lfloor\frac{n}{i}\rfloor$，显然一堆一堆数箱子总数就是 $\sum\lfloor\frac{n}{i}\rfloor$。

但是，如果我们横着数每一层有多少箱子，我们同样可以得到一样的结果：

– 第 1 层：$n$个箱子
– 第 2 层：因为 $\forall i\in[1,\lfloor\frac{n}{2}\rfloor]$都有 $\lfloor\frac{n}{i}\rfloor\ge 2$，所以第二层有 $\lfloor\frac{n}{2}\rfloor$个箱子
– 第 i 层：$\lfloor\frac{n}{i}\rfloor$个箱子

所以箱子总数也可以算出是 $\sum\lfloor\frac{n}{i}\rfloor$

​ 然而为什么要这样变形呢？因为对于某一段连续的 $i$，$\lfloor \frac{n}{i} \rfloor$的值可能是相同的。总共存在的这样的段数可以证明是 $\sqrt{n}$级别的。

定理 1：$\lfloor \frac{n}{i} \rfloor$的取值有 $O(\sqrt{n})$个

证明 1：对于任意相邻的 $i,j\in[1,\sqrt{n}]$，$\lfloor \frac{n}{i} \rfloor$和 $\lfloor \frac{n}{j} \rfloor$都是不小于 $\sqrt{n}$的数。不难看出，$\lfloor \frac{n}{i} \rfloor$和 $\lfloor \frac{n}{j} \rfloor$之间的数对应的 $\lfloor \frac{n}{x} \rfloor$不是 $i$就是 $j$。因此 $\lfloor \frac{n}{i}\rfloor$的取值在 $[1,\sqrt{n}]$和 $(\sqrt{n},n]$之间分布的数量都不会超过 $\sqrt{n}$。

​ 这样，对于每一段连续相等的 $\lfloor\frac{n}{i}\rfloor$，直接用该值与对应 $i$的和相乘即可。

例题：$\sum_{i=1}^{n} \phi(i)$

​ 杜教筛的精髓便在于利用有关被求和函数的某些容易求和的公式，通过之前说的换个角度看问题的方法求得函数前缀和。

​ 对于欧拉函数的前缀和，我们可以利用欧拉函数的一个性质：
$$
\sum_{d|n}\phi(d)=n
$$

​ 这个性质可以看成是：$\phi(n)=n-\sum_{d|n,d < n}\phi(d)$，即将 $n$减去所有与他不互质的数的个数，就是与他互质的数的个数。设 $S(n)=\sum_{i=1}^{n}\phi(i)$。

​ 有了这个性质，我们可以知道：
$$
\sum_{i=1}^{n}\sum_{d|i}\phi(d)=\frac{n\cdot(n+1)}{2}
$$
​ 利用之前说过的" 换个角度" 法，可以推出：
$$
\sum_{i=1}^{n}\sum_{d|i}\phi(d)=\sum_{d=1}^n\lfloor\frac{n}{d}\rfloor\cdot \phi(d)=\sum_{i=1}^n\sum_{j=1}^{\lfloor\frac{n}{i}\rfloor}\phi(j)
$$
​ 因此：
$$
S(n)=\sum_{i=1}^{n}\phi(i)=\frac{n\cdot(n+1)}{2}-\sum_{i=2}^n\sum_{j=1}^{\lfloor\frac{n}{i}\rfloor}\phi(j)=\frac{n\cdot(n+1)}{2}-\sum_{i=2}^nS(\lfloor\frac{n}{i}\rfloor)
$$

​ 这里，原问题 $S(n)$被分解为了 $\sqrt{n}$ 个子问题的和，可以证明，这时时间复杂度已经小于 $O(n)$ 了，约为 $O(n^{\frac{3}{4}})$。

复杂度证明：

我们使用同一法来简单证明。总时间复杂度可以看成是所有在递归过程中出现过的 n 对应的时间复杂度的和。

显然并不是每一个 $[1,n]$ 之间的数都出现了，具体哪些出现了呢？大致是所有 $\lfloor\frac{n}{i}\rfloor$

在每个 $\lfloor\frac{n}{i}\rfloor$上花费的时间又是 $O(\sqrt{\lfloor\frac{n}{i}\rfloor})$ 的，因此：
$$
T(n)=\sum_{i=1}^{\sqrt{n}}\sqrt{\frac{n}{i}}+\sqrt{i}
$$
显然这个式子中 $\sqrt{i}$ 的项每一项都不大于 $\sqrt{\frac{n}{i}}$ 的项，因此可以忽略。

那么
$$
T(n)=\sum_{i=1}^{\sqrt{n}}\sqrt{\frac{n}{i}}\le \int_1^\sqrt{n}\frac{\sqrt{n}}{\sqrt{x}}=2\sqrt{n}\sqrt{\sqrt{n}}=O(n^{\frac{3}{4}})
$$

​ 进一步优化，我们可以让时间复杂度减少到 $O(n^{\frac{2}{3}})$

​ 如果我们用线性筛预处理出前 $O(n^t)$ 个 $S$ 的值，那么上面的积分适就可以写成：
$$
\int_{1}^{n^{1-t}}\frac{\sqrt{n}}{\sqrt{x}}=O(n^{1-0.5t})
$$
​ 显然，当 $O(n^t)=O(n^{1-0.5t})$ 时时间复杂度最优，为 $O(n^{\frac{2}{3}})$，t 取 $\frac{2}{3}$。

例题：$\sum_{i=1}^{n} \mu(i)$

​ 同样的，我们找一个与 $\mu$ 有关的容易求和的公式：
$$
\sum_{d|n}\mu(d)=[n=1]
$$
​ 与之前的步骤一样：
$$
\sum_{i=1}^{n}\sum_{d|i}\mu(d)=\sum_{i=1}^{n}S(\lfloor\frac{n}{i}\rfloor)
$$
​ 所以
$$
S(n)=1-\sum_{i=2}^{n}S(\lfloor\frac{n}{i}\rfloor)
$$
​ 但是也要注意，并不是所有函数都可以利用一个有关整除的求和公式就可以了，有时还是需要对函数性质细致的分析得到一些稍微奇怪一点但是依旧可以用的公式。

题目

1. 莫比乌斯函数之和 (51nod1244)

公式推导已在上文中给出，下面只给出代码

#include <ext/pb_ds/assoc_container.hpp>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <map>
#define MX 4641589

using namespace std;
using namespace __gnu_pbds;

typedef long long ll;

int miu[MX],prm[MX],vis[MX],sum[MX],pnum;
gp_hash_table<ll,bool> has;
gp_hash_table<ll,ll> real;

void init()
{
    miu[1]=1;
    for(int i=2;i<MX;i++)
    {
        if(!vis[i])prm[++pnum]=i,miu[i]=-1;
        for(int j=1;prm[j]*i<=MX&&j<=pnum;j++)
        {
            int k=prm[j]*i;
            vis[k]=1;
            if(i%prm[j]==0)
            {
                miu[k]=0;
                break;
            }
            else miu[k]=miu[prm[j]]*miu[i];
        }
    }
    for(int i=1;i<MX;i++)sum[i]=sum[i-1]+miu[i];
}

ll fuck(ll x)
{
    if(x<MX)return sum[x];
    else if(has[x])return real[x];
    else
    {
        ll ans=1;
        for(ll p=2,q=(x/(x/p));;p=q+1,q=(x/(x/p)))
        {
            ans-=(q-p+1)*fuck(x/p);
            if(q==x)break;
        }
        has[x]=1;
        real[x]=ans;
        return ans;
    }
}

int main()
{
    init();
    ll L,R;
    scanf("%lld%lld",&L,&R);
    printf("%lld\n",fuck(R)-fuck(L-1));
    return 0;
}

2. 循环之美 (NOI2016)

​ 给定 n,m,k，求有多少对 i,j 满足 $\frac{i}{j}$在 k 进制下是纯循环小数 ($n,m\le10^9,k\le2000$)。

​ 题目可以转化为：
$$
\sum_{i=1}^{n}\sum_{j=1}^{m}[(i,j)==1]\cdot[(j,k)==1]
$$
​ 这个公式有多种变形方式，可以从两个方括号中的任意一个入手。下面给出直接从第二个方括号入手的解答。
$$
\begin{aligned}
f(n,m,k) = & \sum_{i=1}^{n}\sum_{j=1}^{m}[(i,j)==1]\cdot[(j,k)==1]\\
= & \sum_{d|k}\mu(d)\sum_{i=1}^n\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[(i,jd)=1]\\
= & \sum_{d|k}\mu(d)\sum_{i=1}^n\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[(i,j)=1]\cdot[(i,d)=1]\\
= & \sum_{d|k}\mu(d)f(\frac{m}{d},n,d)
\end{aligned}
$$
​ 这个式子形式和杜教筛很像，但是由于 n 和 m 的出现，对于每一个 k 并不是只需要计算一次，而是会有多组用到的 f 的 k 相等但 n,m 不相等。可以证明其复杂度是低于 $O(\omega(k)^2)$的。其中 $\omega(k)$为 k 的因子个数

​ $f$的递归出口是 $k=1$或 $n=0$。当 k 等于 1 时，我们需要求互质的 $i,j$对数，这个是一个简单的莫比乌斯反演。
$$
\begin{aligned}
f(n,m,1) & =\sum_{i=1}^n\sum_{j=1}^m[(i,j)=1]\\
& =\sum_{d=1}^n\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor
\mu(d)\end{aligned}
$$
​ 这个函数貌似可以用数论分块 $O(\sqrt{n})$求解，前提是我们需要提前知道 n 以内 $\mu(d)$的前缀和。这尼玛就很恶心了。就算我们用杜教筛，时间复杂度仍然会达到可怕的 $O(n^{7/6})$。但是并不是这样的。

​ 我们之前说到说杜教筛真正用到的 $S(d)$只有那几个 $S(\lfloor\frac{n}{i}\rfloor)$，而这里的所有 $f(x)$的 $x$也都是 $\lfloor\frac{n}{i}\rfloor$ ，所以杜教筛的复杂度完全没有提高。

​ 那么这个算法的时间复杂度就是 $O(\omega(k)^2+n^{2/3})$

​ 不过，下面的代码是基于拆第一个方括号的方法的。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#define MX 1000001
#define MK 2002
#define MD 1423333

using namespace std;

typedef long long ll;

int prm[MX],vis[MX],miu[MX],phi[MX],pnum;
int sum[MX],rem[MX];

struct HASH
{
    int fst[MD],nxt[MX],hnum;
    ll num[MX],real[MX];
    ll exist(ll x)
    {
        int d=x%MD;
        for(int i=fst[d];i;i=nxt[i])
            if(real[i]==x)
                return num[i];
        return -1;
    }
    void insert(ll x,ll s)
    {
        int d=x%MD;
        nxt[++hnum]=fst[d];
        fst[d]=hnum;
        real[hnum]=x;
        num[hnum]=s;
    }
}H,G;

void init(int k)
{
    miu[1]=1,phi[1]=1;
    for(int i=2;i<MX;i++)
    {
        if(!vis[i])prm[++pnum]=i,miu[i]=-1,phi[i]=i-1;
        for(int j=1;j<=pnum;j++)
        {
            int x=prm[j]*i;
            if(x>=MX)break;
            vis[x]=1;
            if(i%prm[j]==0)
            {
                miu[x]=0;
                phi[x]=phi[i]*prm[j];
                break;
            }
            else miu[x]=-miu[i],phi[x]=phi[i]*(prm[j]-1);
        }
    }
    for(int i=1;i<MX;i++)sum[i]=sum[i-1]+miu[i];
    for(int i=1;i<MK;i++)rem[i]=rem[i-1]+(__gcd(i,k)==1);
}

ll cal_sum_miu(int x)
{
    ll ans;
    if(x<MX)return sum[x];
    else if((ans=H.exist(x))!=-1)return ans;
    else
    {
        ans=1;
        int d=2,q;
        while(d<=x)
        {
            q=x/(x/d);
            ans-=(ll)(q-d+1)*cal_sum_miu(x/d);
            d=q+1;
        }
        H.insert(x,ans);
        return ans;
    }
}

ll cal_g(int k,int x)
{
    ll ans=0;
    if(x<=0)return 0;
    else if(k==1)return cal_sum_miu(x);
    else if((ans=G.exist((ll)k+(ll)x*10000))!=-1)return ans;
    else
    {
        ans=0;
        for(int i=1;i*i<=k;i++)
        {
            if(k%i==0)
            {
                ans+=(ll)miu[i]*miu[i]*cal_g(i,x/i);
                if(i*i!=k)ans+=(ll)miu[k/i]*miu[k/i]*cal_g(k/i,x/(k/i));
            }
        }
        G.insert((ll)k+(ll)x*10000,ans);
        return ans;
    }
}

ll calc(int n,int m,int k)
{
    ll ans=0;
    int d=1,q;
    ll pre=0,tmp;
    while(d<=n&&d<=m)
    {
        int t=n/d,p=m/d;
        q=min(n/t,m/p);
        tmp=cal_g(k,q);
        ans+=(ll)t*(phi[k]*(p/k)+rem[p%k])*(tmp-pre);
        pre=tmp;
        d=q+1;
    }
    return ans;
}

int main()
{
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    init(k);
    printf("%lld\n",calc(n,m,k));
    return 0;
}