【算法】树状数组 —— by juruo-oier

下面代码与字都是蒟蒻自己一个一个字打得，如有错误，请大佬指出（我实在太菜了）
这有神犇 boish 的树状数组心得
写得比这一篇好多了

前置知识：搞懂树状数组

树状数组最基本的操作：单点修改 ( $logN$ )+区间查询 ( $logN$ )，上方已经有了，这里就不提了；
其实树状数组还有很多作用

废话不多讲，先看题【模板】树状数组 2

其实这就是

区间修改+单点查询

这利用差分思想
原本：设差分数组 $b[i]=a[i]-a[i-1]$ ，则 $a[i]=b[1]+…+b[i] (b[1]=a[1]-a[0],a[0]=0)$

b[1]+...+b[i]这个东西是不是很熟悉？
没错，这就前缀和

如何快速的求和，这就用树状数组存处差分数组即可

那么如何修改？

设要修改的区间是 $[x，y]$ 加上 k

我们 b 数组是差分数组，差分的修改只要在 x 处加 k，y+1 处减 k 就行了

同理在树状数组上进行同样操作,code:

void add(int x, long long num) {
    while (x <= n) {
        tree[x]+=num;
        x += lowbit(x);
    }
}
long long query(int x) {
    long long ans = 0;
    while (x) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}

时间复杂度：区间修改 ( $logN$ ) 与单点求和 ( $logN$ )

（滑稽的分割线）

区间修改+区间查询

线段树 1
看到这个，一定会想到线段树，可蒟蒻不会，只好用树状数组（其实代码挺短的）

这里还是运用差分思想
区间修改还是和以前一样
那么如何查询？？？
我们来看式子

$a[1]+a[2]+…+a[n]$
$= (c[1]) + (c[1]+c[2]) + … + (c[1]+c[2]+ … +c[n])$

利用乘法分配率：可以得
$n * c[1] + (n-1) * c[2] + … +c[n]$
然后就得到了神奇的式子~高能预警

$\color{red}{n * (c[1]+c[2]+…+c[n]) – (0 * c[1]+1 * c[2]+…+(n-1) * c[n])}$

由公式可以发现我们要进行区间修改和区间查询只需要再维护一个数组 $C2[i] = (i-1) * C[i]$ 即可

代码如下：

#include<bits/stdc++.h>
using namespace std;
long long n,m,tree[100005],tree1[100005];
inline void add(long long*z,long long x,long long num){
    while(x<=n)z[x]+=num,x+=x&(-x);
}
inline long long getsum(long long*z,long long x){
    long long sum=0;
    while(x>0)sum+=z[x],x-=x&(-x);
    return sum;
}
int main(){
    scanf("%lld%lld",&n,&m);
    long long a,b=0;
    for(long long i=1;i<=n;i++)cin>>a,b=a-b,add(tree,i,b),add(tree1,i,(i-1)*b),b=a;
    for(long long i=1;i<=m;i++){
        int t,x,y,z;
        cin>>t;
        if (t==1){
            cin>>x>>y>>z;
            add(tree,x,z);
            add(tree,y+1,-z);
            add(tree1,x,z*(x-1));
            add(tree1,y+1,-z*y);
        }
        else{
            cin>>x>>y;
            cout<<(y*getsum(tree,y)-getsum(tree1,y))-((x-1)*getsum(tree,x-1)-getsum(tree1,x-1))<<endl;
        }
    }
    return 0;
}

区间最值

先看题：
I Hate It
很多人都认为，树状数组不能求解最值，那是应为把树状数组看成前缀和
but，cssyz 金牌教练把树状数组叫做

二进制分块

为啥？
看张图（来自 boshi 大佬）

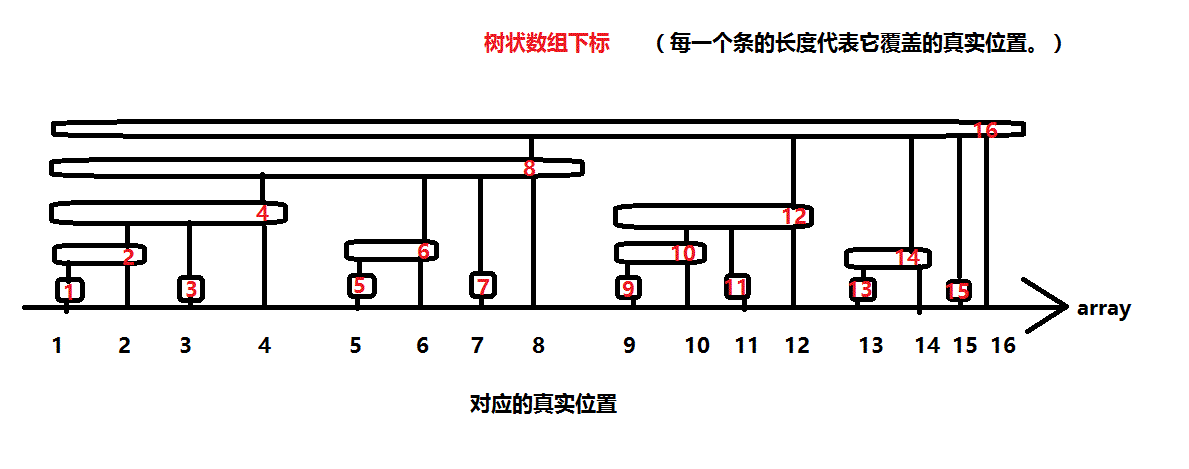
每一个下标，表示的是一块区间
前面求区间和，是把区间合在一起就行了

同理，区间最值也应该是全部块的最大值。

先来看 $[1，n]$ 区间最值
每一个下标，比如 11001000，就是下标 1100xxxx 这些的最大值
我们可以写出这样维护的代码

void add(int n){
     for(int i=1;i<=n;i++){
          c[i]=a[i],int t=lowbit(i);
          for(int j=1;j<t;j*=2) c[i]=max(c[i],c[i-j]);
    }
}

每一次更新一个数时候，把整个树状数组全部更新一遍
但显然，复杂度太高， $O（nlogn）$

我们再想一想：
对于每一个 $c[i]$ ，在保证 $c[1…i-1]$ 都正确的前提下，要重新计算 $c[i]$ 值的时间复杂度是 $O（logn）$
so 我们可以换一种建区间维护方法

void add(int x){
    int lx, i;
    while (x <= n){
        h[x] = a[x];
        lx = lowbit(x);
        for (i=1; i<lx; i<<=1)
            h[x] = max(h[x], h[x-i]);
        x += lowbit(x);
}

显然这个算法的时间复杂度是 $O((logn)^2)$

现在维护好了，问题是如何查询？

直接照搬求区间合的方法显然是不行的。

因为区间合中，要查询 $[x,y]$ 的区间合，是求出 $[1,x-1]$ 的合与 $[1,y]$ 的合，然后相减就得出了 $[x,y]$ 区间的合。

而区间最值是没有这个性质的，所以只能够换一个思路。
因为 $c[y]$ 表示的是 $[y,y-lowbit(y)+1]$ 的最大值 (看图，就是 $c[y]$ 的区间)。

所以，可以这样求解：

若 $y-lowbit(y) > x$ ，则 $query(x,y) = max( c[y] , query(x, y-lowbit(y)) )$

若 $y-lowbit(y) \leq x$ ，则 $query(x,y) = max( a[y] , query(x, y-1))$

int query(int x, int y){
    int ans = 0;
    while (y >= x){
        ans = max(a[y], ans);
        y --;
        for (; y-lowbit(y) >= x; y-=lowbit(y))
            ans = max(c[y], ans);
    }
    return ans;
}

此处可能有点难理解，多琢磨一下

蒟蒻就是会这些；

但有了这些其实可以做很多（例如，求逆序对….）

4 条评论

juruo-oier · 2018年8月25日 8:29 下午

海星！
其实我写得很烂
并不能讲清楚

XZYQvQ · 2018年8月25日 9:06 下午

对惹。。。XZY 擅自更改了您文章里的一些格式

比如：给式子搞上了数学公式
比如：您的 boshi 打错了

然后还有一些比如 * 号两侧没打空格导致公示显示错误之类的 OvO

juruo-oier · 2018年8月25日 9:26 下午

万分感谢。

XZYQvQ · 2018年8月25日 8:14 下午

Orz 好文

（说明一下因为似乎要禁 jay 所以我就 #define 好文 tql 了）