【算法】萌萌哒的最小割树 ——quhengyi11

最小割树是啥树, 能吃吗 (话说树怎么吃)

最小割树 (Gomory-Hu tree)，是可以将一张网络流图通过膜法变成一棵树的算法，这棵树上两两点之间最小权值的边是原图这两个点的最小割。

你可能会想，最小割辣么多，照你这样说一张图所有点对的最小割的权值只会存在 $n-1$种可能喽？

的确是这样的，别急，我们来认 (gan) 真 (xing) 推 (li) 导 (jie) 一发

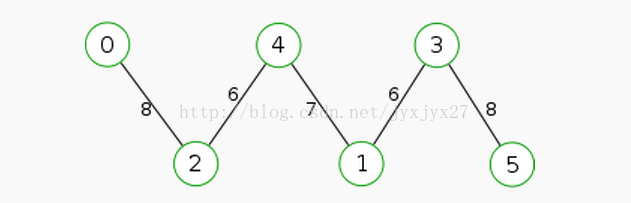
转自 https://blog.csdn.net/jyxjyx27/article/details/42750833(画图还要去用 windows 所以偷懒了)

看上面这棵最小割树，$(4,1)$之间的最小割是 $7$，$(1,3)$之间的最小割是 $6$，我们现在假设 $(4,3)$之间的最小割 $cut<6$，那么将这个最小割割掉之后，原图就会分裂成两个联通块，而点 $1$必然是在其中的一个联通块里的，不妨假设 $1$与 $4$在一个联通块里，那么 $cut$其实也是 $(1,3)$之间的一个割，因为 $cut<6$，所以 $cut$其实是 $(1,3)$之间更小的割，这与原条件矛盾。因此 $(4,3)$之间的最小割不会小于它们在最小割树中的路径里最小的边，而那条最小的边其实是显然可以当作它们的最小割的，因此任意点对之间的最小割是点对在最小割树上的路径中最小的边。因此就至多有 $n-1$条权值不同的最小割。

如果上面的你都看懂了，那么恭喜你，这个算法的核心你已经掌握了，现在的问题就是怎么实现呢？

其实是超简单的啦，你每次在一个元素个数大于等于 2 的联通块里取两个点 $(s,t)$，然后跑一下最小割求出 $cut$，此联通块会被分成两个新的子联通块，而每次分割我们只需要在最小割树中加一条 $(s,t)$权值为 $cut$的边，这样跑 $n-1$次最小割，你就成功地弄出来一棵最小割树啦 (^o^)

让我们来看看例题吧～

CQOI2016 不同的最小割
一道模板题，这道题因为是求最小割的不同权值数，你只要把最小割树上的权值拿出来用 $set$维护一下就行了，根本不需要建树啦
代码：

#include<bits/stdc++.h>
#define fo(i, a, b) for(int i = (a); i <= (b); ++i)
#define N 1805
#define M 18005
#define inf 1000000005
struct edge{
    int to, nxt, w;
}e[M << 1];
int head[N], d[N], u, v, cnt = -1, que[N], a[N], t, n, m, w, rew[M << 1];
std::set <int> s;
inline void addedge(int u, int v, int w)
{
    e[++cnt] = (edge) {v, head[u], w};
    head[u] = cnt;
    rew[cnt] = w;
    e[++cnt] = (edge) {u, head[v], w};
    rew[cnt] = w;
    head[v] = cnt;
}
inline bool bfs (int s, int t)
{
    fo (i, 1, n) d[i] = inf;
    int hh = 1, tt = 1;
    d[s] = 1;
    que[1] = s;
    while (hh <= tt)
    {
        int u = que[hh];
        for (int i = head[u]; i != -1; i = e[i].nxt)
            if (d[e[i].to] == inf && e[i].w)
            {
                ++tt;
                que[tt] = e[i].to;
                d[e[i].to] = d[u] + 1;
            }
        ++hh;
    }
    return d[t] < inf;
}
inline int dfs (int u, int cap)
{
    int used = 0;
    if (u == t) return cap;
    for (int i = head[u]; i != -1; i = e[i].nxt)
        if (d[u] + 1 == d[e[i].to] && e[i].w)
        {
            int ans = dfs(e[i].to, std::min(e[i].w, cap - used));
            if (ans)
            {
                used += ans;
                e[i].w -= ans;
                e[i ^ 1].w += ans;
                if (used == cap) return used;
            }
        }
    if (!used) d[u] = inf;
    return used;
}
inline void solve (int l, int r)
{
    if (l >= r) return;
    int cut = 0;
    t = a[r];
    while (bfs(a[l], a[r])) 
    {
        cut += dfs(a[l], inf);
    }
    s.insert(cut);
    int x = l, y = r;
    while (l < r)
    {
        while (d[a[l]] < inf && l < r) ++l;
        while (d[a[r]] == inf && l < r) --r;
        if (l < r)
        {
            std::swap(a[l], a[r]);
            ++l; --r;
        }
    }
    if (d[a[l]] == inf)  --l;
    fo (i, 0, cnt) e[i].w = rew[i];
    solve(x, l); solve(l + 1, y);
}
int main ()
{
    scanf("%d %d", &n, &m);
    fo (i, 1, n) head[i] = -1;
    fo (i, 1, m)
    {
        scanf("%d %d %d", &u, &v, &w);
        addedge(u, v, w);
    }
    fo (i, 1, n) a[i] = i;
    solve(1, n);
    printf("%d", s.size());
    return 0;
}

再来看下一道题
ZJOI2011 最小割
让你求两两点对最小割中权值小于 k 的有多少个
建一棵最小割树然后暴力维护就行了（我才不会说我因为把 memset(fa, 0, sizeof(fa)) 打成了 memset(fa, sizeof(fa), 0) 调了一个多小时的事的 QAQ）
所以这个代码会比较多的调试信息，祝食用愉快吧。

#include<bits/stdc++.h>
#define fo(i, a, b) for(int i = (a); i <= (b); ++i)
#define fd(i, a, b) for(int i = (a); i >= (b); --i)
#define N 185
#define M 3805
#define inf 1000000005
struct edge{
    int to, nxt, w;
}e[M << 1];
int head[N], d[N], u, v, cnt, que[N], a[N], t, n, m, w, rew[M << 1];
inline void addedge(int u, int v, int w)
{
    e[++cnt] = (edge) {v, head[u], w};
    head[u] = cnt;
    rew[cnt] = w;
    e[++cnt] = (edge) {u, head[v], w};
    rew[cnt] = w;
    head[v] = cnt;  
}
inline bool bfs (int s, int t)
{
    fo (i, 1, n) d[i] = inf;
    int hh = 1, tt = 1;
    d[s] = 1;
    que[1] = s;
    while (hh <= tt)
    {
        int u = que[hh];
        for (int i = head[u]; i != -1; i = e[i].nxt)
            if (d[e[i].to] == inf && e[i].w)
            {
                ++tt;
                que[tt] = e[i].to;
                d[e[i].to] = d[u] + 1;
            }
        ++hh;
    }
    return d[t] < inf;
}
inline int dfs (int u, int cap)
{
    int used = 0;
    if (u == t) return cap;
    for (int i = head[u]; i != -1; i = e[i].nxt)
        if (d[u] + 1 == d[e[i].to] && e[i].w)
        {
            int ans = dfs(e[i].to, std::min(e[i].w, cap - used));
            if (ans)
            {
                used += ans;
                e[i].w -= ans;
                e[i ^ 1].w += ans;
                if (used == cap) return used;
            }
        }
    if (!used) d[u] = inf;
    return used;
}
struct tedge{
    int to, nxt, w;
}e2[N << 1];
int head2[N], cnt2 = 0, fa[N][10], min[N][10], dep[N], mi[N * N];
int q, k, tot;
inline void addedge2 (int u, int v, int w)
{
//  printf("u = %d v = %d w = %d \n", u, v, w);
    e2[++cnt2] = (tedge) {v, head2[u], w};
    head2[u] = cnt2;
    e2[++cnt2] = (tedge) {u, head2[v], w};
    head2[v] = cnt2;
}
inline void dfs2 (int u, int f)
{
    for (int i = head2[u], v = e2[i].to; i; i = e2[i].nxt, v = e2[i].to)
    {
        if (v == f) continue;
        fa[v][0] = u;
        min[v][0] = e2[i].w;
        dep[v] = dep[u] + 1;
        fo (i, 1, 8)
            if (fa[fa[v][i - 1]][i - 1])
            {
                fa[v][i] = fa[fa[v][i - 1]][i - 1];
                min[v][i] = std::min(min[fa[v][i - 1]][i - 1], min[v][i - 1]);
            }
            else
                break;
        dfs2(v, u);
    }
}
inline int getmin (int x, int y)
{
    if (dep[x] > dep[y]) std::swap(x, y);
    int ret = inf, bit = dep[y] - dep[x];
    fo (i, 0, 8)
        if (bit & (1 << i))
        {
            ret = std::min(ret, min[y][i]);
            y = fa[y][i];
        }
    if (x == y) return ret;
    fd (i, 8, 0)
        if (fa[x][i] != fa[y][i])
        {
            ret = std::min(ret, min[x][i]);
            ret = std::min(ret, min[y][i]);
            x = fa[x][i];
            y = fa[y][i];
        }
    ret = std::min(ret, min[x][0]);
    ret = std::min(ret, min[y][0]);
    return ret;
}
inline void solve (int l, int r)
{
    if (l >= r) return;
    int cut = 0;
    t = a[r];
    while (bfs(a[l], a[r])) 
    {
        cut += dfs(a[l], inf);
    }
    addedge2(a[l], a[r], cut);
    int x = l, y = r;
    while (l < r)
    {
        while (d[a[l]] < inf && l < r) ++l;
        while (d[a[r]] == inf && l < r) --r;
        if (l < r)
        {
            std::swap(a[l], a[r]);
            ++l; --r;
        }
    }
    if (d[a[l]] == inf)  --l;
    fo (i, 0, cnt) e[i].w = rew[i];
    solve(x, l); solve(l + 1, y);
}
int main ()
{
    int TT;
    scanf("%d", &TT);
    while (TT--)
    {
        memset(fa, 0, sizeof fa);
        t = n = m = w = 0;
        q = 0; k = 0;
        scanf("%d %d", &n, &m);
        cnt2 = 0; cnt = -1;
        fo (i, 1, n) head[i] = -1, head2[i] = 0;
        fo (i, 1, m)
        {
            scanf("%d %d %d", &u, &v, &w);
            addedge(u, v, w);
        }
        fo (i, 1, n) a[i] = i;
        solve(1, n);
        dep[1] = 1;
        dfs2(1, 0);
        tot = 0;
        fo (i, 1, n)
            fo (j, i + 1, n)
            {
                mi[++tot] = getmin(i, j);
        //      printf("%d %d %d\n", i, j, getmin(i, j));
            }
/*      fo (i, 1, n)
        {
            printf("%d :", i);
            fo (j, 0, 5)
                printf("%d ", fa[i][j]);
            printf("\n");
        }
*/      std::sort(mi + 1, mi + tot + 1);
    //  fo (i, 1, tot)
    //      printf("%d ", mi[i]);
        scanf("%d", &q);
        fo (i, 1, q)
        {
            scanf("%d", &k);
            int pt = std::upper_bound(mi + 1, mi + tot + 1, k) - mi - 1;
            printf("%d\n", pt);
        }
        printf("\n");
    }
    return 0;
}