本篇模拟退火保证 AC 率 (只要你不是只运气差到极致)
让我们愉悦的学习 QVQ
本来还想学粒子群的,但实在是看不懂那些博客,想起 XYZQvQ dalao 的话。就觉的学个模拟退火就算了吧。不然浪费太多时间了 (毕竟我光看着 XYZQvQ 大佬的写粒子群,就发了半小时的呆,Orz)~
没办法,脑子不是很好使,只好用随机算法
首先 看看百度百科是怎么说明模拟退火算法的
模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法,其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。
模拟退火的原理也和金属退火的原理近似:将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有 “能量”,以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始:每一步先选择一个 “邻居”,然后再计算从现有位置到达 “邻居” 的概率。
当一个问题的方案数量极大(甚至是 INF)而且不是一个单峰函数时,我们 (经常)使用模拟退火求解。
简单来说,模拟退火就是模拟将 金属加热到一定温度,保持足够时间,然后以适宜速度冷却。
此算法在寻找到一个局部最优解时,赋予了它一个跳出去的概率,所以也就有更大的机会能找到全局最优解。
具体就是每次随机出一个新解,如果这个解更优,则接受它,否则以一个与温度和与最优解的差相关的概率接受它。
设这个新的解与最优解的差为 $ΔE$,温度为 $T$,$k$为一个随机数,那么这个概率大约为 $exp (ΔE/KT)$
那么我们再看看该算法的简单叙述
首先模拟退火算法 要有一个求解的函数(calc_energy() 也就是模拟金属退火的系统能量), 再就是模拟退火的核心 SA(),以 rand()函数 随机出在解的可行域 中的随机参数 ,再运行 calc_energy() 函数 ,判断得出的答案哪一个最优。如果得出的答案不如原来的优的话,就以上述的概率接受这个新解(为了跳出局部最优)
注意
有时候模拟退火是不适用的:
当函数的峰特别多,所以我们要用分块模拟退火的做法。
大致算法是:将其分为几块,然后对每块跑一遍 SA,最后再合并答案。
然而好像没有要用这个的题。不过万一以后考了呢
这里块的数量不是 $sqrt(n)$ , 而是一个比较小的数。要根据不同的题用不同的大小。
START
初始化温度 $T_0$(最大可能的解,本题 $T_0$=2500,具体看题目你确定的解的范围,不过过大也不会对算法优太大影响)
降温系数 $ΔT 0 $ (一般是略大于 0)
然后 运行就是 先令 $T=T_0$ ,再每次 $T~=~T~*~ΔT$ 直到 $T<T_k$ 为止
这完美的退火算法演示 qwq
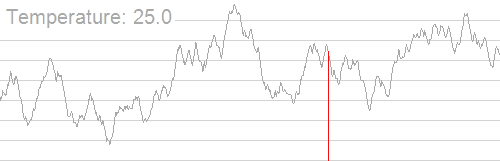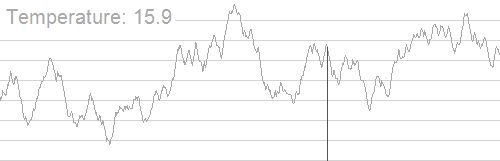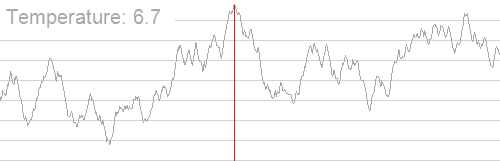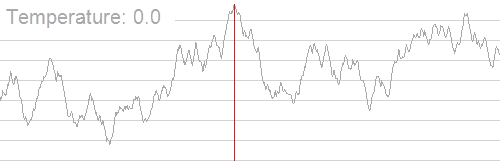
可以看到该算法先是找到一个局部最优,然后以一定概率,跳出这个范围,再一直循环找到局部最优。
但是如果有时没找到最优解的话,那么你可以调大 $ΔT$ 和 $T_0$,或者调小终止温度 $T_k $;
再不然你可以更改随机种子
个人推荐:
srand(time(0));
srand(rand());
srand(rand());
while ((double)clock()/ CLOCKS_PER_SEC < 0.7) SA();//0.7~= 700ms
// 在你程序快超时为止一直运行 SA(),注意根据你程序的快慢 修改 0.7;
随机中的随机 QVQ
如果还是不行的话
抱歉,这一切都是命运石之门的选择
如何生成新解
- 坐标系内:随机生成一个点,或者生成一个向量。
- 序列问题:$random\_shuffle$或者随机交换两个数。
- 网格问题:可以看做二维序列,每次交换两个格子即可。
那么我们再来看看例题吧,不过主要是用其它算法得出解再模拟退火而已
First :题解 P1337【[JSOI2004] 平衡点 / 吊打 XXX】
本题算是模拟退火的经典吧。
我写的这篇模拟退火虽然运行时间较长,但 AC 率非常之高 (在 T 与 AC 之间徘徊)因为是在保证不 T 的情况下,一直运行 SA()
本题题解大多是模拟退火,所以我就不再多说了,详情见代码
因为物重一定,绳子越短,重物越低,重力势能就越小,重力势能势能又与物重成正比,所以,只要使得总的重力势能最小,就可以使系统平衡
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <cstdlib>//必备头文件
using namespace std;
#define fors(i,a,b) for(int i=(a);i<=(b);++i)
typedef long long ll;
const int Size=1<<4;
inline char getch(){
static char buf[Size],*p1=buf,*p2=buf;
return p1==p2 && (p2=(p1=buf)+fread(buf,1,Size,stdin),p1==p2) ? EOF : *p1++;
}
int read(){
int s=0,f=1;
char c=getch();
while(c>'9' || c<'0'){if(c=='-') f=-1;c=getch();}
while(c<='9' && c>='0'){s=(s<<1)+(s<<3)+c-'0';c=getch();}
return s*f;
}
void write(int x){
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
#define max(x,y) ((x) > (y) ? (x) : (y))
#define min(x,y) ((x) < (y) ? (x) : (y))
const int maxn=1e5+7;
struct node
{
int x,y,w;
}a[maxn];
//以上皆为卡常
int n,sx,sy;
double ansx,ansy;
double ans=1e18,t;//解的范围
double delta=0.997;
double cal(double x,double y){
double rt=0;
fors(i,1,n){
double tmpx=x-a[i].x,tmpy=y-a[i].y;
rt+=sqrt(tmpx*tmpx + tmpy*tmpy)*a[i].w;//计算重力势能
}
return rt;
}
void SA(){
t=2500;
double x=ansx,y=ansy;
while(t>1e-14){
double tmpx=x+((rand()<<1)-RAND_MAX)*t;
double tmpy=y+((rand()<<1)-RAND_MAX)*t;//创造新解
double now=cal(tmpx,tmpy),flag=now-ans;
if(flag < 0){//如果差值小于零 ,OK
ans=now,ansx=tmpx,ansy=tmpy;
}
else if(exp(-flag/t)*RAND_MAX > rand())//以一个概率修改
x=tmpx,y=tmpy;
t*=delta;//修改温度
}
}
void AC(){
ansx=(double)sx/n,ansy=(double)sy/n;//平均值更接近正解
while((double)clock()/CLOCKS_PER_SEC < 0.83) SA();//直到你快 T 了为止一直运行
}
int main(){
srand(233333);
n=read();
srand(rand());//玄学的 srand
fors(i,1,n){
a[i].x=read(),a[i].y=read(),a[i].w=read();
sx+=a[i].x,sy+=a[i].y;//累加
}
AC();
printf("%.3lf %.3lf",ansx,ansy);
return 0;
}
【题解】LUOGU UVA10228 A Star not a Tree?
题意:给定一个 N 边形所有顶点坐标 x,y,求其费马点到所有顶点距离和
费马点是指到多边形所有顶点距离和最小的点
事实上这题 在洛谷上的提交非常毒瘤,(每组数据要多输出一个换行,最后一组不用)要不是看到题解的 dalao 说了,我绝对不知道
求到多边形所有顶点距离和最小的点
我脑子不好使,就随机取点,模拟退火
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <ctime>
#include <cstdlib>
using namespace std;
#define fors(i,a,b) for(int i=(a);i1e-6){
int n;
double xx,yy,ans,t;
struct point{
double x,y;
}p[105];
double sqr(double x){
return x*x;
}
double dis(double x,double y,point p){
return sqrt(sqr(x-p.x)+sqr(y-p.y));
}
double cal(double x,double y){
double tmp=0;
fors(i,1,n)
tmp+=dis(x,y,p[i]);
return tmp;
}
void SA(){
double tmp,x,y;
while(t>1e-6){
x=y=0;
fors(i,1,n){
x+=(p[i].x-xx)/dis(xx,yy,p[i]);
y+=(p[i].y-yy)/dis(xx,yy,p[i]);
}//在范围内构造新参数
tmp=cal(xx+x*t,yy+y*t);
if(tmp<ans){
ans=tmp;xx+=x*t,yy+=y*t;
}
else if(exp(-(tmp-ans)/t)*RAND_MAX > rand()){
ans=tmp;xx+=x*t,yy+=y*t;
}
t*=0.993;
}
}
int main()
{
srand(time(0));
srand(rand());
int ks;
cin>>ks;
fors(lk,1,ks){
cin>>n;
memset(p,0,sizeof p);
xx=yy=0;ans=1e20;t=1e6;
fors(i,1,n){
scanf("%lf%lf",&p[i].x,&p[i].y);
xx+=p[i].x;yy+=p[i].y;//累加 xx,yy
}
xx/=n;yy/=n;//为了从平均解开始
ans=cal(xx,yy);
SA();//先开始运行一次
while((double)clock()/CLOCKS_PER_SEC < (1.0/(ks+1))) SA();
printf("%.0lf",ans);
if (lk!=ks) printf("\n");
}
return 0;
}
4 条评论
Remmina · 2019年2月15日 8:36 下午
突然发现代码里使用了
clock,这在 NOI 系列赛事中似乎是不被允许的请阅读这篇文章的同学注意一下哦
CraZYali · 2018年11月5日 9:55 下午
Orz
让我第一次深刻理解,太感谢了。
XZYQvQ · 2018年9月23日 10:39 下午
Orz 大佬劲啊 Orz
感谢大佬在本站发文 QwQ
B_Z_B_Y · 2018年9月24日 10:35 上午
QvQ Orz