前言

orz 一下这位大神。

本文献给想要性感地理解支配树的同学，如果你想更性感一点，所有证明均可跳过。

litble 特别菜，有错误请指出，谢谢。

支配点

很久很久以前，有一张有向图，有向图有一个起点 $S$ ，有一个叫小 X 的强盗，占据一个点拦路打劫。当小 X 占据了 $x$ 点后，若从 $S$ 出发就到不了 $y$ 点了，那么 $x$ 就是 $y$ 的支配点。

而支配树，就是满足树上一个点 $x$ 的所有祖先都是它的支配点的树。

How to build 支配树

以下我们假定从 $S$ 出发可以到达图上所有点。

树形图

显然，树形图自己就是自己的支配树。

DAG

DAG 的话，我们按照拓扑序从小到大进行，假设处理到点 $x$ ，则查一遍所有可达点 $x$ 的点 $y$ ，所有点 $y$ 一定被加入了支配树中，那么它们在支配树上的 LCA 就是 $x$ 在支配树上的父亲。

倍增就可以做到 $O(n \log n)$ ，例题洛谷 P2597，代码如下：

#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
const int N=65540;
int n,top,js;
int f[N][16],du[N],p[N],st[N],ans[N],dep[N];
vector<int> g[N],rg[N],tr[N];
void topsort() {
    for(RI i=1;i<=n;++i)
        if(!du[i]) g[0].push_back(i),rg[i].push_back(0),++du[i];
    top=1,st[top]=0;
    while(top) {
        int x=st[top];p[++js]=x,--top;
        for(RI i=0;i<g[x].size();++i) {
            --du[g[x][i]];
            if(!du[g[x][i]]) st[++top]=g[x][i];
        }
    }
}
int lca(int x,int y) {
    if(dep[x]<dep[y]) swap(x,y);
    for(RI i=15;i>=0;--i) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
    if(x==y) return x;
    for(RI i=15;i>=0;--i) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
void dfs(int x) {
    ans[x]=1;
    for(RI i=0;i<tr[x].size();++i)
        dfs(tr[x][i]),ans[x]+=ans[tr[x][i]];
}
int main()
{
    n=read();
    for(RI i=1;i<=n;++i) {
        int x=read();
        while(x) g[x].push_back(i),rg[i].push_back(x),++du[i],x=read();
    }
    topsort();
    for(RI i=2;i<=n+1;++i) {
        int x=p[i],y=rg[x][0];
        for(RI j=1;j<rg[x].size();++j) y=lca(y,rg[x][j]);
        tr[y].push_back(x),dep[x]=dep[y]+1,f[x][0]=y;
        for(RI j=1;j<=15;++j) f[x][j]=f[f[x][j-1]][j-1];
    }
    dfs(0);
    for(RI i=1;i<=n;++i) printf("%d\n",ans[i]-1);
    return 0;
}

一般有向图

一般有向图有一个优秀的做法叫做 Lengauer Tarjan，对，又是 Tarjan，Tarjan tql。

首先，我们从 $S$ 开始 dfs 整张图，可以提取出一棵 dfs 树，并且 $x$ 的 dfs 序是 $dfn(x)$ 。

半支配点

假设存在一个点 $y$ ，从 $y$ 出发有一条到 $x$ 的路径，并且路径上任何一点 $z$ （不包括 $x$ 和 $y$ ）都满足 $dfn(z)>dfn(x)$ ，则称 $y$ 为 $x$ 的半支配点。

记 $semi(x)$ 为 $x$ 的 dfn 最小的半支配点，因为 $x$ 在 dfs 树上的父亲也是它的一个半支配点，所以 $semi(x)$ 一定是 $x$ 的祖先。

我们为什么需要这个 $semi$ 呢？因为我们删掉原图中的非树边后，连边 $(semi(x),x)$ ，不改变原图中的支配点关系。性感的证明如下：

假如在原图上删掉 $y$ ， $x$ 就不可达了，那么显然 $y$ 是 $x$ 在 dfs 树上的祖先。
假若从 $y$ 的某个祖先出发，可以在不经过 $y$ 的情况下，走到一个 $dfn(y) < dfn(z) \leq dfn(x)$ 的点 $z$ ， $y$ 就是 $x$ 的支配点，反之不是。
因为不能经过 $y$ ，所以从这个祖先走到 $z$ 的路径上经过的所有点的 $dfn$ 应该大于 $y$ 。
假如这条路径上的所有点的 $dfn$ 都大于 $z$ ，则显然通过 $(semi(z),z)$ 可以保证新图上这个点依然能到 $z$ 。否则，这条路径要么经过一个 $dfn$ 小于等于 $x$ 大于 $y$ 的点（直接满足条件），要么全部经过 $dfn$ 大于 $x$ 的点（也就是 $x$ 的半支配点）
所以，新图中的支配点关系与原图相同。

如果求出了 $semi$ ，我们就把原图变成了一个 DAG，然后就可以重复 DAG 的做法啦。不过更优的做法也是有的。

求半支配点

对于一个点 $x$ ，我们找到所有边 $(y,x)$ 对应的 $y$ 。

若 $dfn(y)<dfn(x)$ 且 $dfn(y)$ 比当前找到的 $semi(x)$ 的 $dfn$ 小，则用 $semi(x)=y$ 。

若 $dfn(y)>dfn(x)$ ，找到树上 $y$ 的一个祖先 $z$ ，且 $dfn(z)>dfn(x)$ ，比较 $dfn(semi(z))$ 和 $dfn(semi(x))$ 的大小，决定是否用 $semi(z)$ 更新 $semi(x)$ 。

性感的证明就是：

考虑从 $semi(x)$ 到 $x$ 的那条只经过 $dfn$ 大于 $x$ 的点的路径上， $x$ 的前驱。若这个前驱是一个 $dfn$ 小于 $x$ 的点，那么只有可能从这个点出发是满足条件的。
否则，这条路径上可能经过 $dfn$ 小于 $y$ 且大于 $x$ 的点（因为已经证明原图缩成 DAG 合法，所以不可能从 $dfn$ 大于 $y$ 的点走过来啦 QvQ），枚举这些点 $z$ ，它们的 $semi$ 就是满足条件的 $semi$ 。

从半支配点到支配点

对于 $x$ ，我们要求它在支配树上的父亲，也就是 $idom(x)$ 。

寻找方法如下：

我们记 $P$ 为从 $semi(x)$ 到 $x$ 的树上路径点集（不包括 $semi(x)$ ），而 $z$ 是 $P$ 中 $dfn(semi(z))$ 最小的点。若 $semi(z)=semi(x)$ ，则有 $idom(x)=semi(x)$ ，否则有 $idom(x)=idom(z)$ 。

对于前半句性感的证明就是，没有 $semi(x)$ 的祖先连到 $P$ 中的边，则删去 $semi(x)$ ， $x$ 就不可达。

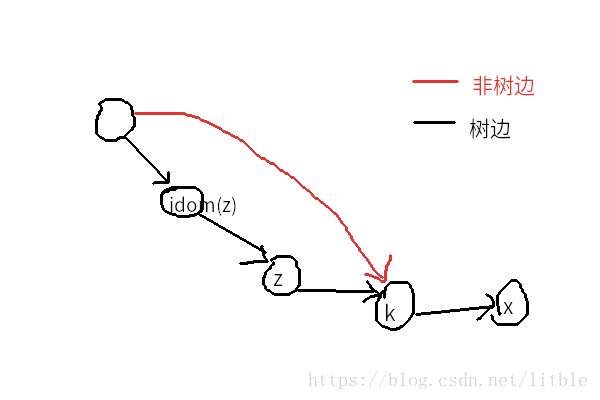
对于后半句性感的证明（见下图）就是：

假设删掉 $idom(z)$ ， $x$ 依旧可达，则说明在 dfs 树上， $idom(z)$ 有一个祖先，可以走一条非树边（也就是通过 semi 连出来的边，图中红边）到达 $x$ 到 $idom(z)$ 中间的一个点 $k$ 。
若 $z$ 不是 $k$ 的祖先，则删掉 $idom(z)$ 后 $z$ 仍可达，与支配点定义不符，所以 $z$ 是 $k$ 的祖先。
那么因为 $z \in P$ （我希望你还记得 $P$ 的定义），所以 $k \in P$ 。因为删除 $idom(z)$ 后 $semi(z)$ 不可达，所以 $dfn(semi(k)) \leq dfn(idom(z)) \leq dfn(semi(z))$ ，与我之前定义的 “ $z$ 是 $P$ 中 $dfn(semi(z))$ 最小的点” 矛盾，所以该假设不可能成立。

灵魂画手litble

算法流程

那么具体怎么实现呢？其实很简单——用带权并查集！

首先安装 dfs 序从大到小处理，每次处理完毕一个点后，将这个点与它 dfs 树上的父亲在并查集连边。而并查集带的权，就是并查集中这个点到根节点的路径上的所有点， $dfn(semi(x))$ 最小的 $x$ 是哪个。

找 $semi$ 直接找即可，找 $idom$ 则在 $semi(x)$ 处处理 $x$ 的信息即可。

（Tarjan 大神很喜欢 dfs 树和并查集啊）

例题：HDU4694（起点为 $n$ ，求每个点支配的点的编号和）
Wraning: 数据出错，对于 $n$ 无法到的点，答案为 0，并且清空边集的时候，与 0 相连的边集也要清空（MDZZ 调了劳资一下午）

#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
    int q=0;char ch=' ';
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
    return q;
}
typedef long long LL;
const int N=50005,M=100005;
int n,m,tim;
int dfn[N],repos[N],mi[N],fa[N],f[N],semi[N],idom[N],ans[N];
struct graph{
    int tot,h[N],ne[M],to[M];
    void clear() {tot=0;for(RI i=0;i<=n;++i) h[i]=0;}//此题数据有误所以应从 i=0 开始清空
    void add(int x,int y) {to[++tot]=y,ne[tot]=h[x],h[x]=tot;}
}g,rg,ng,tr;

void init() {
    tim=0;g.clear(),rg.clear(),ng.clear(),tr.clear();
    for(RI i=1;i<=n;++i)
        repos[i]=dfn[i]=idom[i]=fa[i]=ans[i]=0,mi[i]=semi[i]=f[i]=i;
}
void tarjan(int x) {
    dfn[x]=++tim,repos[tim]=x;
    for(RI i=g.h[x];i;i=g.ne[i])
        if(!dfn[g.to[i]]) fa[g.to[i]]=x,tarjan(g.to[i]);
}
int find(int x) {
    if(x==f[x]) return x;
    int tmp=f[x];f[x]=find(f[x]);
    if(dfn[semi[mi[tmp]]]<dfn[semi[mi[x]]]) mi[x]=mi[tmp];
    return f[x];
}
void dfs(int x,LL num) {
    ans[x]=num+x;
    for(RI i=tr.h[x];i;i=tr.ne[i]) dfs(tr.to[i],num+x);
}
void work() {
    for(RI i=n;i>=2;--i) {
        int x=repos[i],tmp=n;
        for(RI j=rg.h[x];j;j=rg.ne[j]) {
            if(!dfn[rg.to[j]]) continue;//此题数据有误
            if(dfn[rg.to[j]]<dfn[x]) tmp=min(tmp,dfn[rg.to[j]]);
            else find(rg.to[j]),tmp=min(tmp,dfn[semi[mi[rg.to[j]]]]);
        }
        semi[x]=repos[tmp],f[x]=fa[x],ng.add(semi[x],x);

        x=repos[i-1];
        for(RI j=ng.h[x];j;j=ng.ne[j]) {
            int y=ng.to[j];find(y);
            if(semi[mi[y]]==semi[y]) idom[y]=semi[y];
            else idom[y]=mi[y];//此时 idom[mi[y]] 可能并未找到
        }
    }
    for(RI i=2;i<=n;++i) {
        int x=repos[i];
        if(idom[x]!=semi[x]) idom[x]=idom[idom[x]];
        tr.add(idom[x],x);
    }
    dfs(n,0);
}
int main()
{
    int x,y;
    while(~scanf("%d%d",&n,&m)) {
        init();
        for(RI i=1;i<=m;++i)
            x=read(),y=read(),g.add(x,y),rg.add(y,x);
        tarjan(n);work();
        for(RI i=1;i<n;++i) printf("%d ",ans[i]);
        printf("%d\n",ans[n]);
    }
    return 0;
}

【算法】性感理解支配树　——litble

于2018年10月12日2018年10月12日由litble发布

前言

支配点

How to build 支配树

树形图

DAG

一般有向图

半支配点

求半支配点

从半支配点到支配点

算法流程

litble

5 条评论

孤月 · 2020年6月14日 4:58 下午

XZYQvQ · 2018年10月13日 11:01 上午

B_Z_B_Y · 2018年10月13日 8:22 上午

boshi · 2018年10月12日 8:59 下午

litble · 2018年10月12日 9:26 下午

回复 litble 取消回复

【算法】性感理解支配树 ——litble

于2018年10月12日2018年10月12日由litble发布

前言

支配点

How to build 支配树

树形图

DAG

一般有向图

半支配点

求半支配点

从半支配点到支配点

算法流程

litble

5 条评论

孤月 · 2020年6月14日 4:58 下午

XZYQvQ · 2018年10月13日 11:01 上午

B_Z_B_Y · 2018年10月13日 8:22 上午

boshi · 2018年10月12日 8:59 下午

litble · 2018年10月12日 9:26 下午

回复 litble 取消回复

【算法】性感理解支配树　——litble