0. 引言
在计算几何中,经常要求判断线段与线段或直线是否有交点。如果简单地求它们的交点再进行判断容易出错(误差之类的,而且比较麻烦),所以我们需要稳定的方法来判断!
- 注:后文中所有的表示未标注的话均为向量表示法。
1. 法一(基本法曰.. 曰)
定义
- 一条直线由一个点 $O$和一个向量 $V$组成,过点 $O,P$的直线可以表示为:$O+kV$,其中 $V=\overrightarrow{OP}$。
- $O=(x,y),P=(x1,y1),\overrightarrow{OP}=(x1-x,y1-y)$
- 一条线段由两个点构成
1. 判断线段与直线相交
正文
点 p2 对于线段的关系可以分为 5 种,如图所示:
- 1.$\overrightarrow{p0p2}$在 $\overrightarrow{p0p1}$逆时针方向 (Counter Clock Wise)
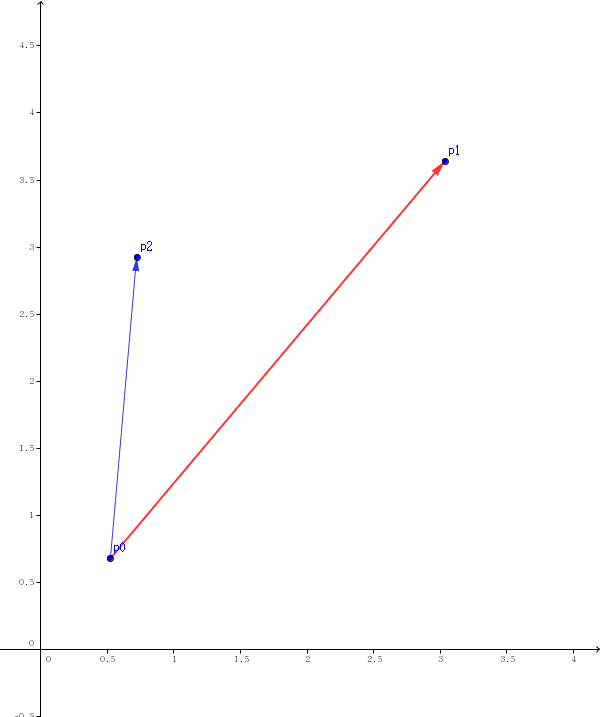
- 2.$\overrightarrow{p0p2}$在 $\overrightarrow{p0p1}$顺时针方向 (Clock Wise)
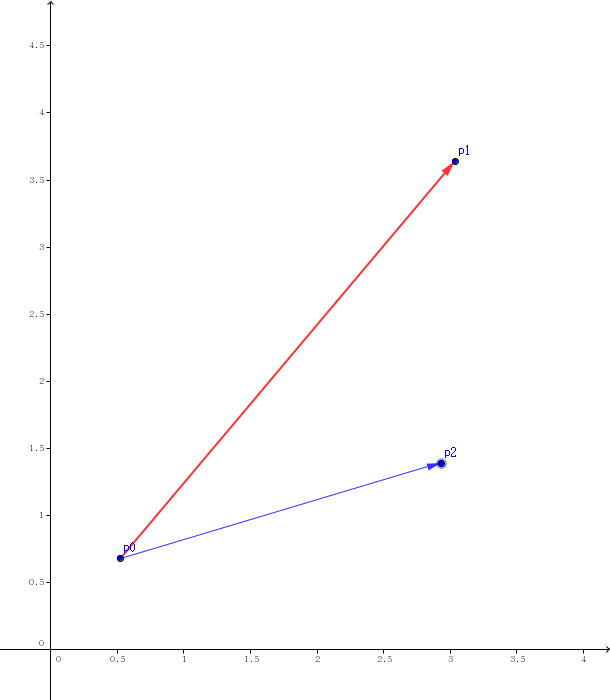
- 3.$p2$在直线 $p0p1$上且 $\overrightarrow{p0p1}$与 $\overrightarrow{p0p2}$反向 (On Line Back)
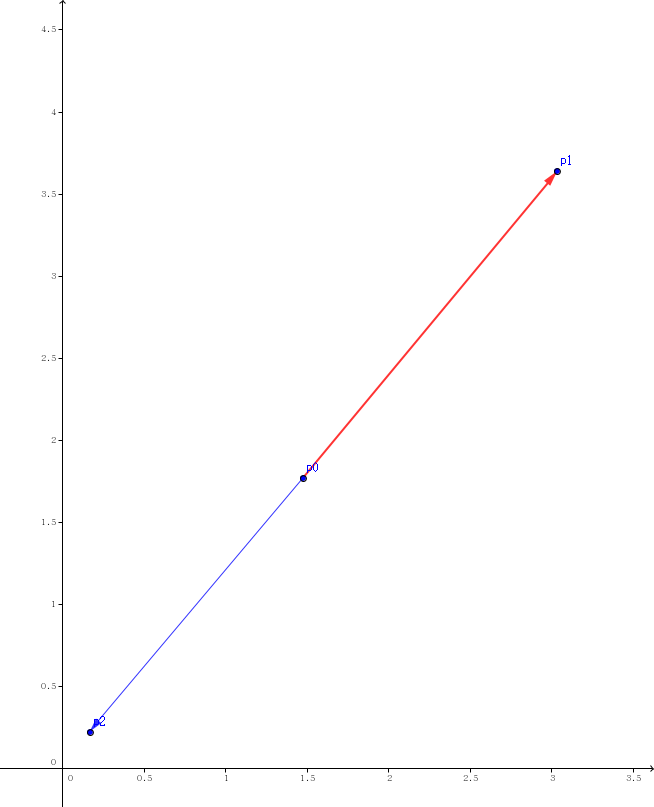
- 4.$p2$在直线 $p0p1$上且 $\overrightarrow{p0p1}$与 $\overrightarrow{p0p2}$同向且 $p2$不在线段 $p0p1$上 (On Line Front)
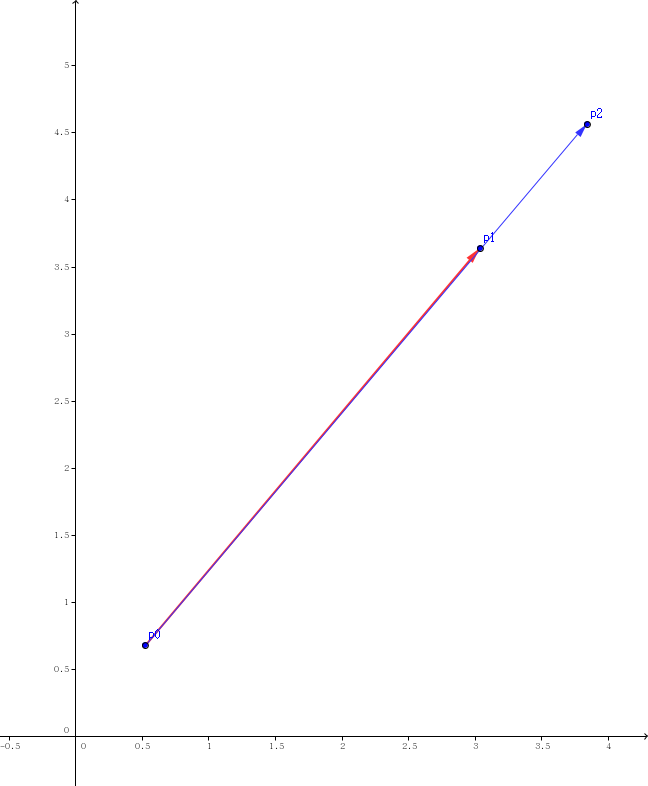
- 5.$p2$在直线 $p0p1$上且 $\overrightarrow{p0p1}$与 $\overrightarrow{p0p2}$同向且 $p2$在线段 $p0p1$上 (On segment)
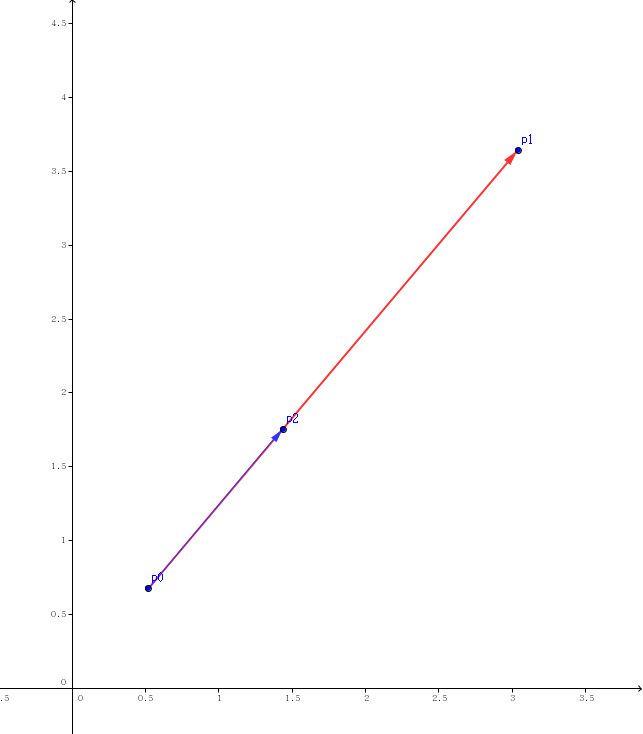
那么我们就可以分类讨论他们的特点啦。
首先,如果两条线段($p0p1$与 $p2p3$)相交,则对于 $p0,p1$来说有如下三种情况:
- $p0,p1$分别在 $\overrightarrow{p2p3}$两端,一个在顺时针方向,一个在逆时针方向。
- $p0,p1$中至少有 1 个在线段 $p2p3$上
- $p0,p1,p2,p3$在同一直线上,且线段 $p2,p3$在线段 $p0,p1$上
对于 $p2,p3$同理。
于是我们需要判断一个点与一条线段之间的关系。
然后我们就写了这样一个函数(下面的情况指的是上面五张图中的各种情况):
#define EPS (1e-10)
typedef struct Point//点与向量的结构体
{
double x,y;
double dot(Point a){return x*a.x+y*a.y;}//点乘
double cross(Point a){return x*a.y-a.x*y;}//叉乘
double norm(){return x*x+y*y;}//计算向量大小
Point operator - (Point a){return (Point){x-a.x,y-a.y};}//向量相减
}Vector;
double ccw(Point s,Point e,Point p)//Counter Clock wise, 判断点与线段的位置关系
{
//s 是线段起点,e 是终点,p 是需要判断的点
Vector a=e-s,b=p-s;//那么这里的 a 就上面五张图中红色的向量,b 是蓝色的向量
if(a.cross(b)>EPS)return 1;//若 a 与 b 的叉积为正就说明是情况 1,即点在线段逆时针方向
if(a.cross(b)<-EPS)return -1;//若 a 与 b 的叉积为负就说明是情况 2,即点在线段顺时针方向
//剩下三种情况为点在线段所在直线上
if(a.dot(b)<-EPS)return 2;//若 a 与 b 的点积为负,则说明两向量反向,为情况 3
if(a.norm()<b.norm())return -2;//若 a 的大小小于 b 的大小,说明是情况 4
return 0;//点在线段上,情况 5
}
代码也不长,可以准确判断点与线段关系。
注意一下函数的返回值。
为什么要一正一负呢?仔细观察:
- $p0,p1$分别在 $\overrightarrow{p2p3}$两端,一个在顺时针方向,一个在逆时针方向。此时 $ccw(p2,p3,p0)\times ccw(p2,p3,p1)=-1$
- $p0,p1$中至少有 1 个在线段 $p2p3$上,此时 $ccw(p2,p3,p0)\times ccw(p2,p3,p1)=0$
- $p0,p1,p2,p3$在同一直线上,且线段 $p2,p3$在线段 $p0,p1$上,此时 $ccw(p2,p3,p0)\times ccw(p2,p3,p1)=-4$
发现没有?我们利用了异号相乘为负和任何数乘以 $0$均为 $0$的性质,如果 $ccw(p2,p3,p0)\times ccw(p2,p3,p1)\leq 0$则说明对于 $p0,p1$满足上面的三个条件。
而这时候还不足以说明 $p0p1$与 $p2p3$相交,还需要判断对于 $p2,p3$是否满足上面的三个条件。
所以判断两条线段 $p0p1$与 $p2p3$是否相交的代码如下(intersect,相交,若相交返回 true(1)):
bool intersect(Point p0,Point p1,Point p2,Point p3)
{
return (ccw(p0,p1,p2)*ccw(p0,p1,p3)<=0&&ccw(p2,p3,p0)*ccw(p2,p3,p1)<=0);
}
例题
You can Solve a Geometry Problem too
HDU – 1086: 传送门= ̄ω ̄=
题意:给出 $n$条线段,判断有几对线段相交。
代码:
#include <bits/stdc++.h>
#define EPS (1e-10)
using namespace std;
typedef struct Point
{
double x,y;
double dot(Point a){return x*a.x+y*a.y;}
double cross(Point a){return x*a.y-a.x*y;}
double norm(){return x*x+y*y;}
Point operator - (Point a){return (Point){x-a.x,y-a.y};}
}Vector;
int n,ans;
Point ps[105],pe[105];
double ccw(Point s,Point e,Point p)
{
Vector a=e-s,b=p-s;
if(a.cross(b)>EPS)return 1;
if(a.cross(b)<-EPS)return -1;
if(a.dot(b)<-EPS)return 2;
if(a.norm()<b.norm())return -2;
return 0;
}
bool intersect(Point p0,Point p1,Point p2,Point p3)
{
return (ccw(p0,p1,p2)*ccw(p0,p1,p3)<=0&&ccw(p2,p3,p0)*ccw(p2,p3,p1)<=0);
}
int main()
{
while(scanf("%d",&n),ans=0,n)
{
for(int i=1;i<=n;i++)
scanf("%lf%lf%lf%lf",&ps[i].x,&ps[i].y,&pe[i].x,&pe[i].y);
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
ans+=intersect(ps[i],pe[i],ps[j],pe[j]);
printf("%d\n",ans);
}
return 0;
}
2. 判断线段与直线相交
正文
这个问题比判断线段与线段相交简单些。
比如判断直线 $S+kV$和线段 $p0p1$是否相交,只需要判断 $p0p1$与 $S+kV$的位置关系。
思路与上面一样,只不过是 $ccw$函数不需要判断第 3,4 种情况(指的是上面的那 5 张图所示的情况),即我们把这两种情况均视为第 5 种情况——点在直线上。
所以 $ccw$函数这么写:
int ccw(Point s,Vector v,Point p)//判断直线 s+kv 与点 p 的关系
{
Vector v2=p-s;
if(v.cross(v2)>EPS)return 1;//点在直线逆时针方向
if(v.cross(v2)<-EPS)return -1;//点在直线顺时针方向
return 0;//点在直线上
}
而且其实我们的 $intersect$函数也要改:
bool intersect(Point s,Vector v,Point p1,Point p2)
{
return (ccw(s,v,p1)*ccw(s,v,p2)<=0);
}
于是就愉快地判断了线段与直线关系啦!
例题
Segments
POJ – 3304: 传送门= ̄ω ̄=
题解:枚举任意两线段的不同端点,过这两点作一条直线。若存在一条直线与所有线段都相交则存在答案,输出 Yes!。否则说明不存在答案,输出 No!
注意特判只有一条线段的情况。
(我之前把特判写读入前面了WA了好久!
代码:
#include <cstdio>
#include <cmath>
#define NS (105)
#define EPS (1e-10)
using namespace std;
typedef struct Point
{
double x,y;
double cross(Point a){return x*a.y-a.x*y;}
Point operator - (Point a)const{return (Point){x-a.x,y-a.y};}
bool operator != (Point a)const{return fabs(x-a.x)>EPS||fabs(y-a.y)>EPS;}
}Vector;
int T,n;
Point p[2][NS];
int ccw(Point s,Vector v,Point p)
{
Vector v2=p-s;
if(v.cross(v2)>EPS)return 1;
if(v.cross(v2)<-EPS)return -1;
return 0;
}
bool intersect(Point s,Vector v,Point p1,Point p2)
{
return (ccw(s,v,p1)*ccw(s,v,p2)<=0);
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lf%lf%lf%lf",&p[0][i].x,&p[0][i].y,&p[1][i].x,&p[1][i].y);
if(n==1){puts("Yes!");goto nxt;}
Vector v;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int x0=0;x0<=1;x0++)
for(int x1=0;x1<=1;x1++)
if(p[x0][i]!=p[x1][j])
{
v=p[x1][j]-p[x0][i];
for(int k=1;k<=n;k++)
if(!intersect(p[x0][i],v,p[0][k],p[1][k]))goto end;
puts("Yes!");goto nxt;
end:continue;
}
puts("No!");
nxt:continue;
}
return 0;
}
法二 (二次判断法)
对于两个线段是否相交,我们可以用一种较为快速的方法。利用一下几个结论。
- 如果包裹两条线段的矩形没有相交,那么两条线段一定没有相交,反之不一定。(排斥实验)
- 如果线段彼此跨过对方所在的直线或端点在直线上,则两线段一定相交。(跨立实验)
对于线段是否跨过一条直线,我们可以利用向量叉乘判断。叉乘是两向量的一种乘积,其结果 (2 维空间中) 是一个标量。如果我们在 2 维空间中,将两个向量的屁股接在一起,伸出右手,右手食指伸出指向向量 a,再转一个小于 $\pi$的角度指向 b,那么大拇指的方向代表了 $a\times b$的符号。如果大拇指朝上,则符号为正,反之为负。如果大拇指既不朝上也不朝下,那么请去医院检查一下,或者检查一下你是否理解了上面这段话。
所以代码大概是这样的:
typedef struct tvec
{
double x,y;
tvec operator - (const tvec a)const{return (tvec){x-a.x,y-a.y};}
}vec;
double crs(vec a,vec b){return a.x*b.y-a.y*b.x;}
bool Intersect(vec s1,vec e1,vec s2,vec e2)
{
if( min(s1.y,e1.y)>max(s2.y,e2.y)|| //排斥实验
max(s1.y,e1.y)<min(s2.y,e2.y)||
min(s1.x,e1.x)>max(s2.x,e2.x)||
max(s1.x,e1.x)<min(s2.x,e2.x))return 0;
if( crs(s1-e2,s2-e2)*crs(e1-e2,s2-e2)<=0&& //跨立实验
crs(e2-s1,e1-s1)*crs(s2-s1,e1-s1)<=0)return 1;
else return 0;
}
4 条评论
litble · 2018年1月19日 8:24 下午
表示蒟蒻是求个交点然后判断是否在线段上的 QAQ
konnyakuxzy · 2018年1月19日 9:36 下午
你这样会有误差啊
还是图样图森破 QvQ
litble · 2018年1月20日 9:37 下午
Orz 这种方法就是不管是两条什么线相交都可以用这种做法,不用动脑子。
还是您比较强啊
konnyakuxzy · 2018年1月20日 9:38 下午
这说明您的方法就是强啊 Orz
(另外您再改下我的评论试试看?)